Advent of Code Day 11 was a fun one. While part 1 was super easy, part 2 required a bit more work, let’s dive in!

---

The below is a guest post by the amazing Shraddha Agrawal.

---

Part 1

The input is a list of comma separated numbers, each number representing a stone. Every time we blink, stones change. The rules for the change are as follows:

• stone with number 0 gets replaced with a stone with number 1.
• stone with a number that has even count of digits is split into two such that the first stone has the number formed by first half of digits and the second stone has the number with the rest of the digits.
• any other stone is replaced by a stone with the number 2024 time of its current number.

Applying the rules for the initial arrangement of stone, the progression would look like this for 3 blinks:

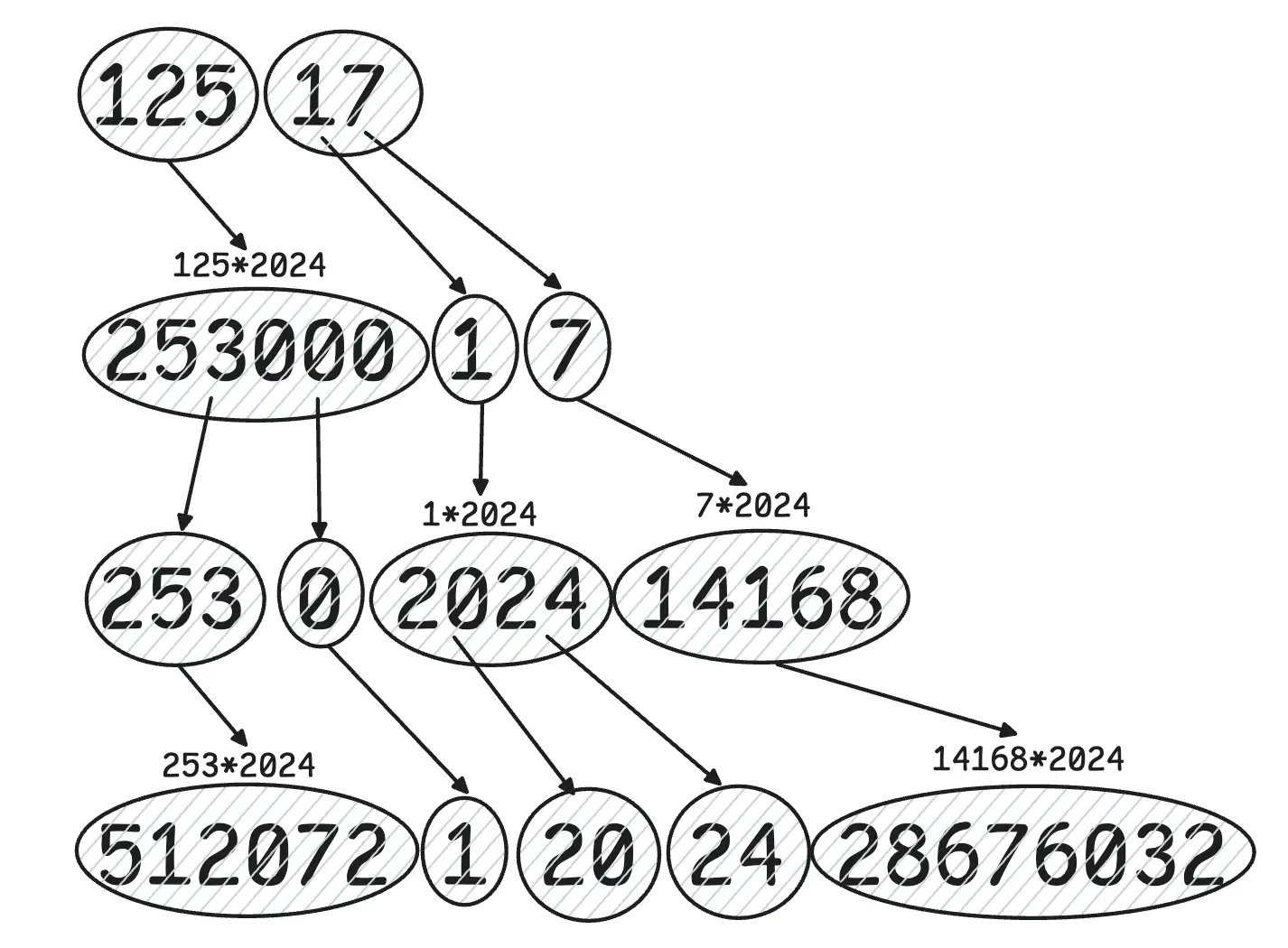
For part 1, we need to return the count of stones after 25 blinks.

Solution

On reading the question carefully, that first thing I noticed was that the sequence of stone is not important only their count after the specified number of blinks. This means we can handle each stone independently and not worry about it’s relative position as compared to other stones.

Let’s start off with writing a function which will process stones after 1 blink, applying the rules as given above.

func getStonesAfterBlink(stone int) []int {
	resultStones := []int{}

	switch {
	case stone == 0:
		resultStones = append(resultStones, 1)
	case len(strconv.Itoa(stone))%2 == 0:
		s1, s2 := splitStone(stone)
		resultStones = append(resultStones, s1, s2)
	default:
		resultStones = append(resultStones, stone*2024)
	}

	return resultStones
}

func splitStone(stone int) (int, int) {
	stoneString := strconv.Itoa(stone)
	stone1, stone2 := stoneString[:len(stoneString)/2], stoneString[len(stoneString)/2:]
	return aoc.FetchNumFromStringIgnoringNonNumeric(stone1), aoc.FetchNumFromStringIgnoringNonNumeric(stone2)
}

Now, its time to calculate how many stones we are left with for each input stone after 25 blinks. As noted above, we are handling each input stone independently. For this, I wrote a simple for loop:

func getCountAfterXBlinks(stone int, blinks int) int {
	stones := []int{stone}

	for _ = range blinks {
		newStones := []int{}
		for _, stone := range stones {
			newStones = append(newStones, getStonesAfterBlink(stone)...)
		}
		stones = newStones
	}
	return len(stones)
}

A point to note here: we are keeping track of the actual stones after each blink and getting the count after all 25 blinks are done. This will become relevant in part two.

We call the above function for each of the input stones and sum the result to find the final answer.

Part 2

This might have been the shortest part 2 problem statement in Advent of Code I have encountered so far! This time instead of 25 blinks we need to get the count after 75 blinks.

Solution

While it seemed quite straightforward, the count of stone quickly explodes as number of blinks increases. The brute force way we are doing to get the answer for part 1 will be too slow to get the answer in a reasonable amount of time for 75 blinks. Time for optimising the part 1 solution!

Armed with the fact that the order of stones don’t matter, a few more observations:

1. For each input stone, instead of keeping track of all stones we get after blinking, keeping the count is sufficient.
2. If we cache the count of stones after X for each stone number, when that number if encountered again, we won’t need to do this calculation again! This is called memoisation.

Lets expand on 2 and see how we can implement this. For each stone, the maximum amount of blinks we will compute is 75. So we can create a map with an int key and an int array (not a slice) with length 75 as the value. For each stone number, we can save the count of stones we have after 1,2,3…. blinks in its respective value slice.

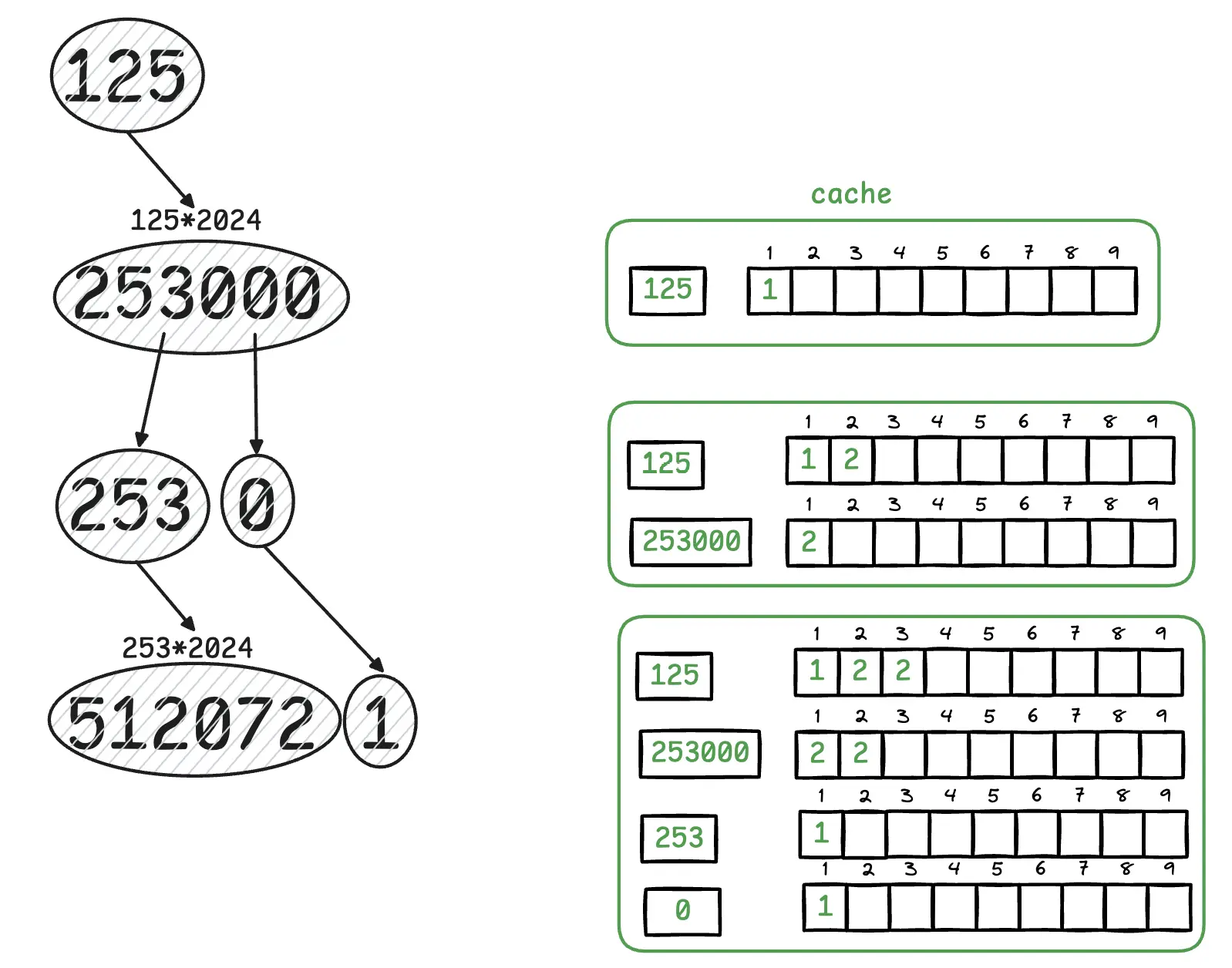
We can write a recursive solution which takes advantage of the above cache we just talked about. This function makes use of the first observation above, where we are keeping track of the number of stones instead of all stones after blinking each time. For this function:

1. Success case: if the input blink count is 1, we can simply call getStonesAfterBlink and return the value (after saving the value in cache).
2. Exit case: Is the input stone number and blink count is present in the cache, simply return the count that is saved in the map.
3. For all other cases, find the stones after 1 blink using getStonesAfterBlink and recursively call the func for each stone. Save the result in cache.

Writing this out:

func getCountAfterXBlinks(stone int, cache map[int][]int, blinkCount int) int {
	if _, ok := cache[stone]; ok {
		if cache[stone][blinkCount-1] != 0 {
			return cache[stone][blinkCount-1]
		}
	} else {
		cache[stone] = make([]int, 75)
	}

	if blinkCount == 1 {
		cache[stone][blinkCount-1] = len(getStonesAfterBlink(stone))
		return len(getStonesAfterBlink(stone))
	}

	sum := 0

	for _, stone := range getStonesAfterBlink(stone) {
		sum += getCountAfterXBlinks(stone, cache, blinkCount-1)
	}

	cache[stone][blinkCount-1] = sum
	return sum
}

And thats it! Calling the above function for each stone in the original input, we can get the answer for part 2. You can find my final code here.

Memoisation is a neat trick to optimise a problem where if we’ve done a computation before, we just use the saved value instead of redoing the calculation. Advent of Code notoriously has always had problems that are more reasonable to solve using this concept than with brute force as was the case here!

How did you approach Day 11? I would love to compare notes and checkout your solution. Reach out to me on Twitter, Bluesky or on e-mail at contact[at]shraddhaag[dot]dev.