Advent of Code Day 12 was a super fun problem navigating a 2D grid and putting to use some polynomial math. Let’s figure it out!

---

The below is a guest post by the amazing Shraddha Agrawal.

---

Part 1

Input is a map of garden plots. A garden region is described as a continuous, connected cells all marked with the same letter, indicating the type of plants.

A couple other rules that apply to garden regions:

1. It is also possible for garden regions to have holes in them.
2. Separate garden regions with the same plants are valid.

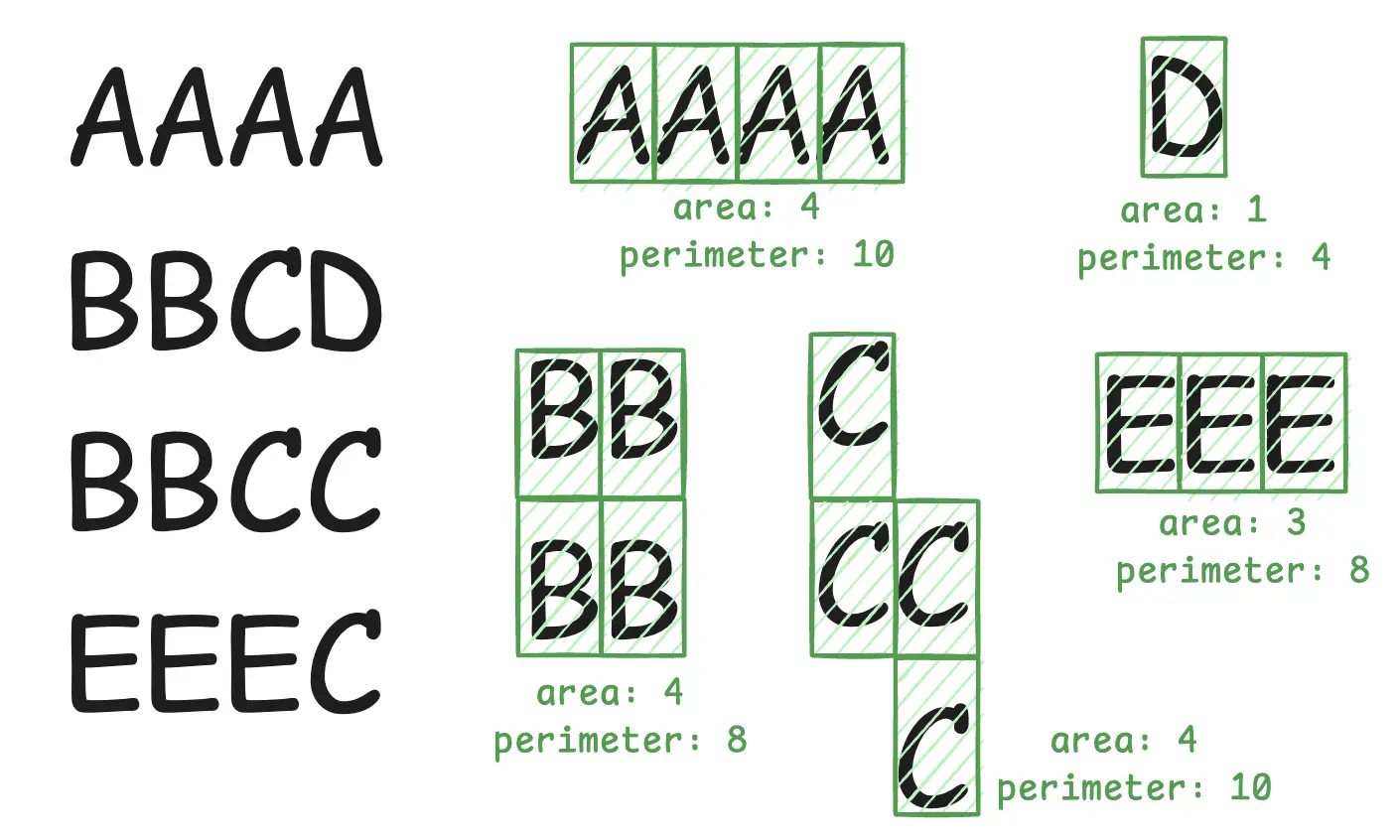
Consider the below example where O garden region has holes in them and there are 4 different garden regions of the same plant X.

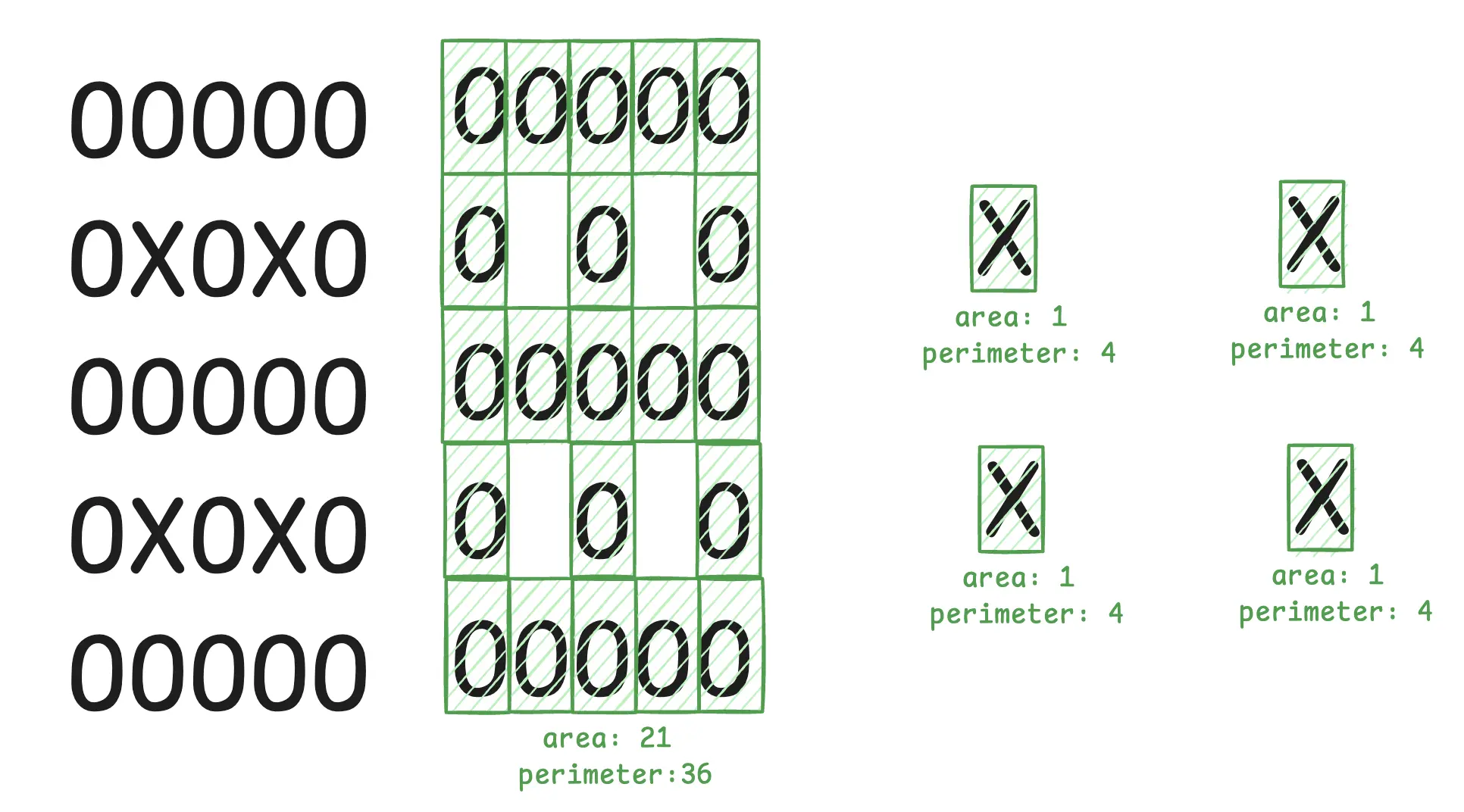
For part 1, we need to find the area and perimeter for each garden region and use them to calculate the cost of fences. The fences cost formulae for a garden region is the product of its area and perimeter. The final answer should be the sum of cost for all garden regions present in the input.

Solution

Seeing the above examples its clear that we can not just simply sum all cells with the same type of plant to find the garden region as same plants can have multiple disconnected garden regions.

I went with an approach similar to flood fill algorithm. We start with a coordinate and check all its 4 neighbours, if any of them are the same type, we recursively check them as well till we encounter no further attached garden plots. A few points:

1. Area of the garden region is equal to the number of cells in the regions. We can figure it out by incrementing area each time the function is called with a cell of the same garden type.

2. To calculate perimeter contribution of each cell, we observe that perimeter is not needed on sides where cells of the same plant type exists. ie,

   1. if a cell is surrounded by the same type of garden plots on all 4 sides, its contribution to perimeter is 0.
   2. if a cell is surrounded by the same type of garden plots on 3 sides, its contribution to perimeter is 1.

   Extrapolating from there, perimeter contribution of a cell = 4 - count of neighbours with same type of garden plot.

3. If all 4 sides do not match with the current cell, it means its a garden region with a single cell.

One last thing before we write the recursive function, to avoid visiting the same cells again and again, we can have a visited map where we record each cell that has already been visited as part of a region.

Now, writing the DFS approach:

func findAllGardensRecursive(input [][]string, current p, shape polynomial, visited map[p]struct{}) polynomial {
	if _, ok := visited[current]; ok {
		return shape
	}

	checkNext := checkAll4(input, current)

	// none surrounding are same garden
	if len(checkNext) == 0 {
		if shape.area == 0 {
			shape.area = 1
			shape.perimeter = 4
			visited[current] = struct{}{}
			return shape
		}
		return shape
	}

	shape.perimeter += 4 - len(checkNext)
	shape.area += 1
	visited[current] = struct{}{}

	for _, next := range checkNext {
		shape = findAllGardensRecursive(input, next, shape, visited)
	}
	return shape
}

And calling the above func for each cell in the input if not already visited:

func ans(input [][]string) (int, int) {
	cost := 0
	visited := make(map[p]struct{})
	for j, row := range input {
		for i, _ := range row {
			if _, ok := visited[p{i, j}]; ok {
				continue
			}
			shape := findAllGardensRecursive(input, p{i, j}, polynomial{}, visited)
			cost += shape.area * shape.perimeter
		}
	}
	return cost
}

And that gives us the final answer for part 1!

Part 2

Now, instead of finding perimeter for the cost, we need to calculate sides of a garden region.

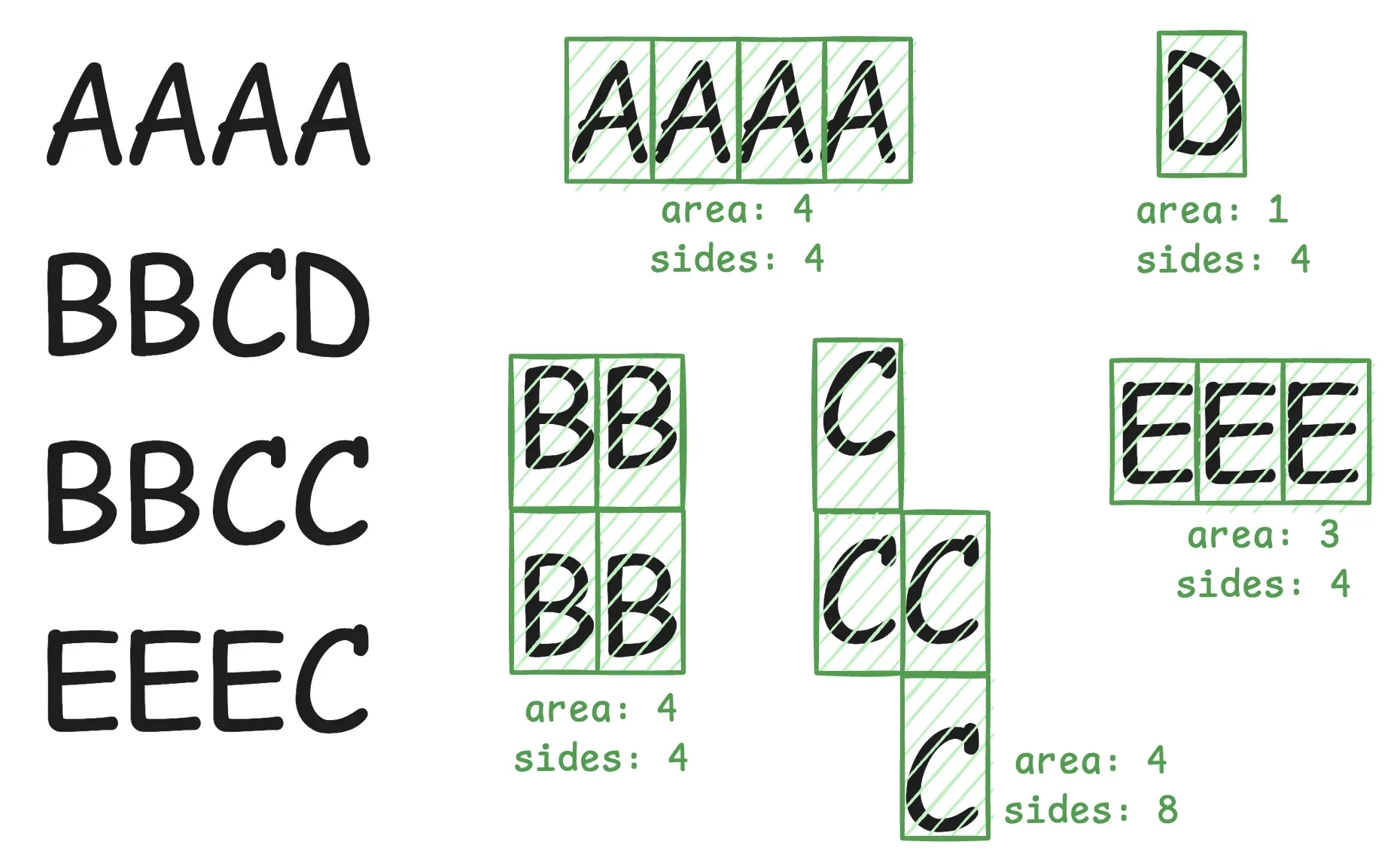
Consider, the first example, the garden regions all have 4 sides, except the garden region with the plant E.

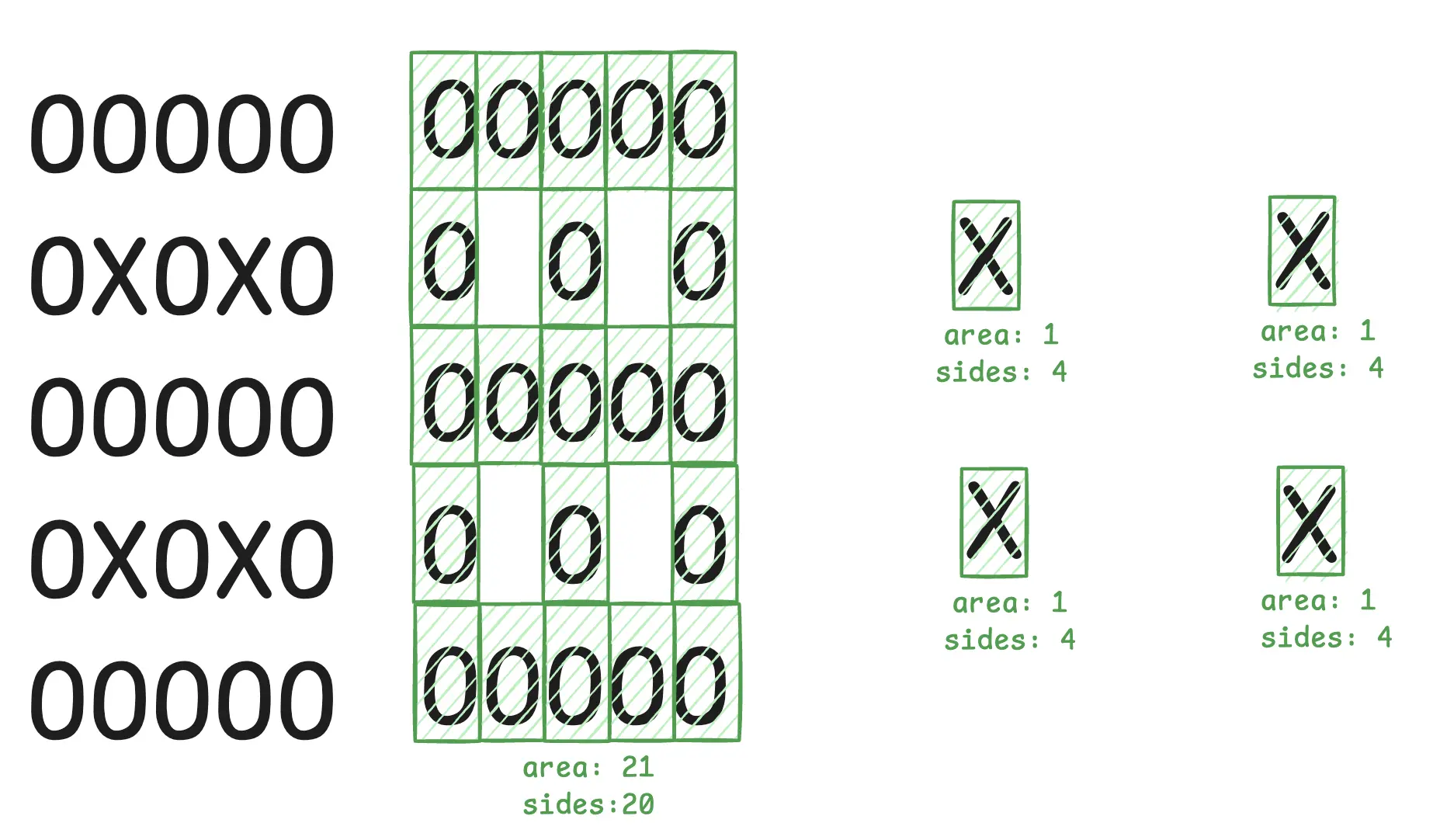
Doing the same for second example, the big garden region with 4 holes has now 20 sides:

• 4 sides for the outer area
• 4 sides each for all 4 holes

The new cost formulae is the product of area and sides. The final answer should be the sum of cost for all garden regions.

Solution

The crux of solving part 2 is figuring out how do we calculate sides for each garden region. I contemplated quite a few different approaches before it hit me: the number of sides is the same as the number of corners in a polygon.

Now, given the coordinates of a polygon, we just need to figure out how many corners does the garden region have. Two points to note here:

1. A garden region can have both outside and inside corners.
2. A single cell can contribute to more than one corner.

I wanted to calculate how many corners a given cell is contributing to, so I sketched out the conditions when a cell is contributing corners. In the below image, O signifies the element is part of the polygon and # are the elements outside the polygon.

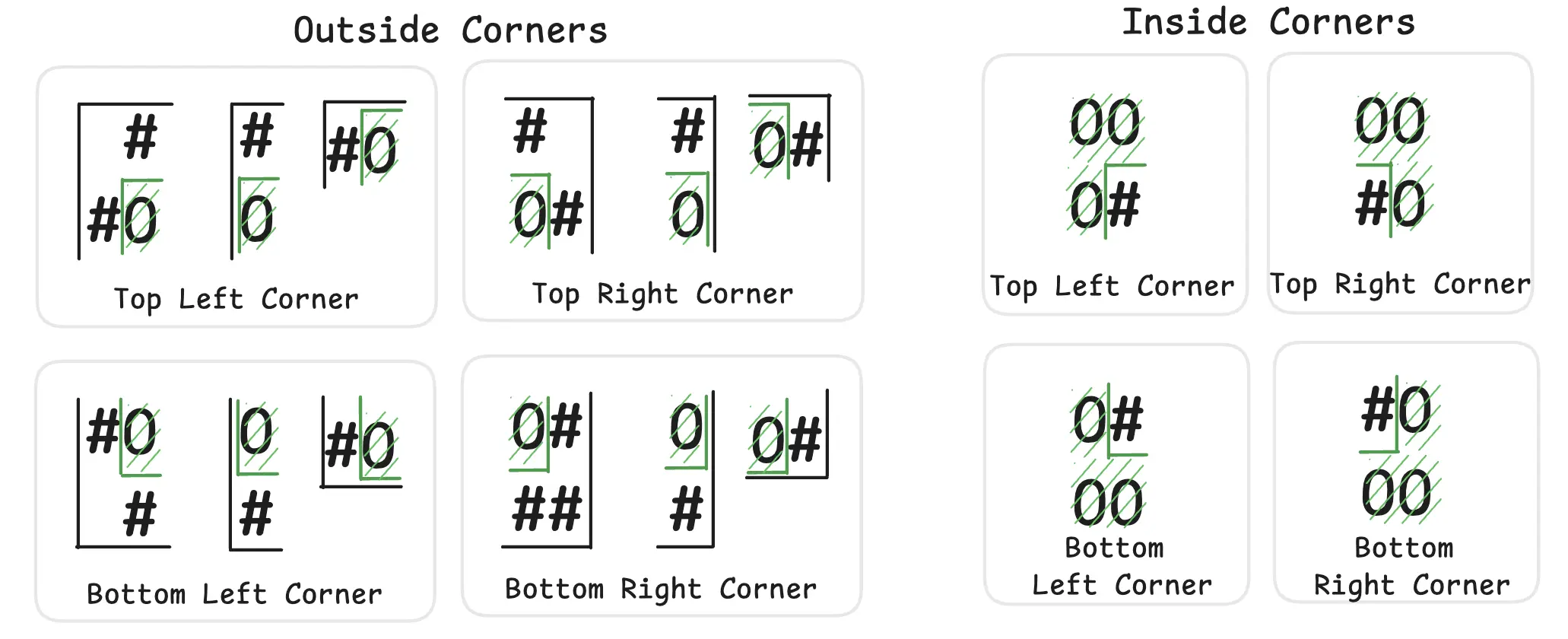
For each cell, if we check the above 8 conditions, we can get the number of corners it is contributing to. I wrote this check quite crudely:

// checkCorners checks if there are any corners on the
// current coordinates. It checks for both, outside
// and inside corners
func checkCorners(input [][]string, current p) int {
	count := 0
	gardenType := input[current.y][current.x]
	x, y := current.x, current.y

	if x == 0 && y == 0 {
		count += 1
	}

	if x == 0 && y == len(input)-1 {
		count += 1
	}

	if x == len(input[0])-1 && y == len(input)-1 {
		count += 1
	}

	if x == len(input[0])-1 && y == 0 {
		count += 1
	}

	// top left outside corner
	// ##   __   |#
	// #O   #O   |O
	if (x > 0 && y > 0 && input[y][x-1] != gardenType && input[y-1][x] != gardenType) ||
		(x > 0 && y == 0 && input[y][x-1] != gardenType) || (x == 0 && y > 0 && input[y-1][x] != gardenType) {
		count += 1
	}

	// top left inside corner
	// OO
	// O#
	if x < len(input[0])-1 && y < len(input)-1 && input[y][x+1] == gardenType && input[y+1][x] == gardenType && input[y+1][x+1] != gardenType {
		count += 1
	}

	// top right outside corner
	// ##   __    #|
	// O#   O#    O|
	if (x < len(input[0])-1 && y > 0 && input[y][x+1] != gardenType && input[y-1][x] != gardenType) ||
		(x < len(input[0])-1 && y == 0 && input[y][x+1] != gardenType) || (x == len(input[0])-1 && y > 0 && input[y-1][x] != gardenType) {
		count += 1
	}

	// top right inside corner
	// OO
	// #O
	if x > 0 && y < len(input)-1 && input[y][x-1] == gardenType && input[y+1][x] == gardenType && input[y+1][x-1] != gardenType {
		count += 1
	}

	// bottom left outside corner
	// #O   #O    |O
	// ##   --    |#
	if (x > 0 && y < len(input)-1 && input[y][x-1] != gardenType && input[y+1][x] != gardenType) ||
		(x > 0 && y == len(input)-1 && input[y][x-1] != gardenType) || (x == 0 && y < len(input)-1 && input[y+1][x] != gardenType) {
		count += 1
	}

	// bottom left inside corner
	// O#
	// OO
	if x < len(input[0])-1 && y > 0 && input[y][x+1] == gardenType && input[y-1][x] == gardenType && input[y-1][x+1] != gardenType {
		count += 1
	}

	// bottom right outside corner
	// O#   O#    O|
	// ##   --    #|
	if (x < len(input[0])-1 && y < len(input)-1 && input[y][x+1] != gardenType && input[y+1][x] != gardenType) ||
		(x < len(input[0])-1 && y == len(input)-1 && input[y][x+1] != gardenType) || (x == len(input[0])-1 && y < len(input)-1 && input[y+1][x] != gardenType) {
		count += 1
	}

	// bottom right inside corner
	// #O
	// OO
	if x > 0 && y > 0 && input[y][x-1] == gardenType && input[y-1][x] == gardenType && input[y-1][x-1] != gardenType {
		count += 1
	}
	return count
}

And finally, we can just call this func for each cell as we are processing it in the above recursive func, with a simple 2 line change:

func findAllGardensRecursive(input [][]string, current p, shape polynomial, visited map[p]struct{}) polynomial {
	if _, ok := visited[current]; ok {
		return shape
	}

	checkNext := checkAll4(input, current)

	// none surrounding are same garden
	if len(checkNext) == 0 {
		if shape.area == 0 {
			shape.area = 1
			shape.perimeter = 4
			visited[current] = struct{}{}
			shape.sides = checkCorners(input, current)
			return shape
		}
		return shape
	}

	shape.perimeter += 4 - len(checkNext)
	shape.area += 1
	visited[current] = struct{}{}
	shape.sides += checkCorners(input, current)

	for _, next := range checkNext {
		shape = findAllGardensRecursive(input, next, shape, visited)
	}
	return shape
}

And that’s it! The new sum is the answer for part 2. You can find my final solution here.

I found this day super interesting and had a lot of fun figuring out how to calculate the sides for each garden region/polygon. I also went ahead and wrote a BFS solution ie non recursive function to identify garden regions. You can find it here.

How did you approach Day 12? I would love to compare notes and checkout your solution. Reach out to me on Twitter, Bluesky or on e-mail at contact[at]shraddhaag[dot]dev.