Advent of Code Day 14 had people divided, some loved the problems and others did not. As for me, I learned a cool way to spot for any image in a 2D grid. Let’s dive in!

---

The below is a guest post by the amazing Shraddha Agrawal.

---

Part 1

Input is a list of robots. Each robot’s initial position and velocity is given. The robots are moving in a space that is 101 tiles wide and 103 tiles tall. The rules for moving are:

• Multiple robots can be present at the same position.
• If the robot is going beyond the edges of the space, they “teleport” on the other side.

Consider the robot with the given configuration p=2,4 v=2,-3. This signifies initial position (2,4) with a velocity (2,-3). Visualising it’s movement for the first 5 seconds we see it “teleports” along the Y and X axis like shown below.

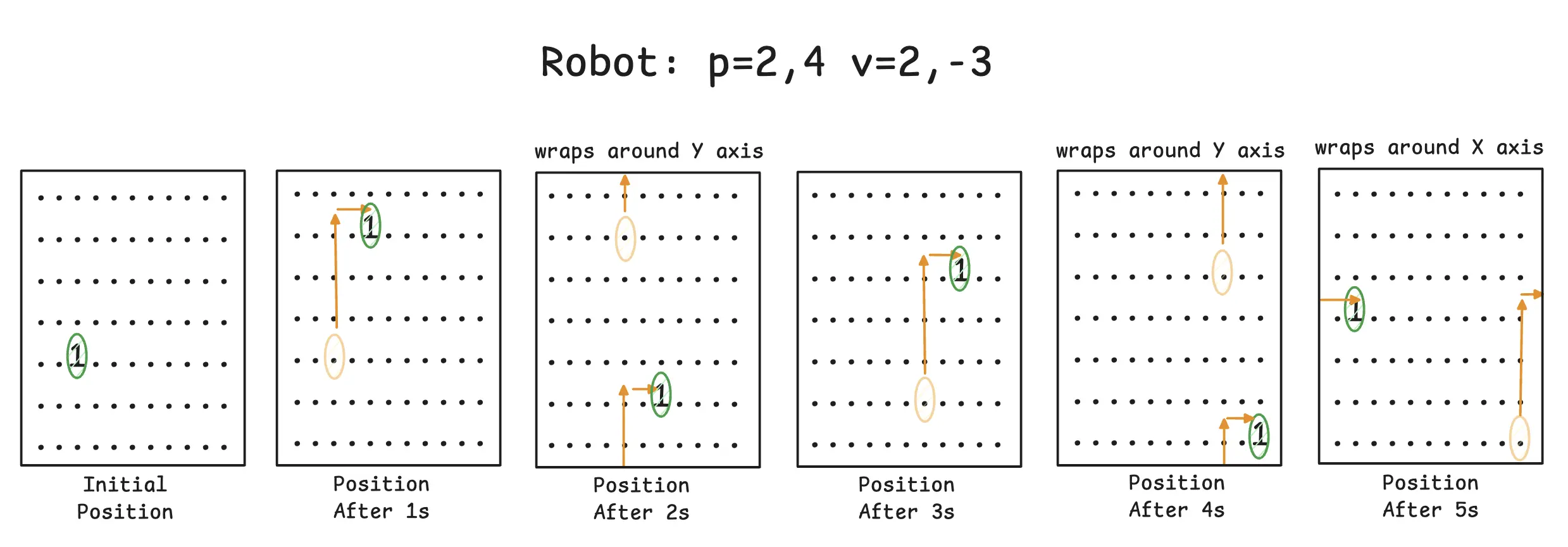
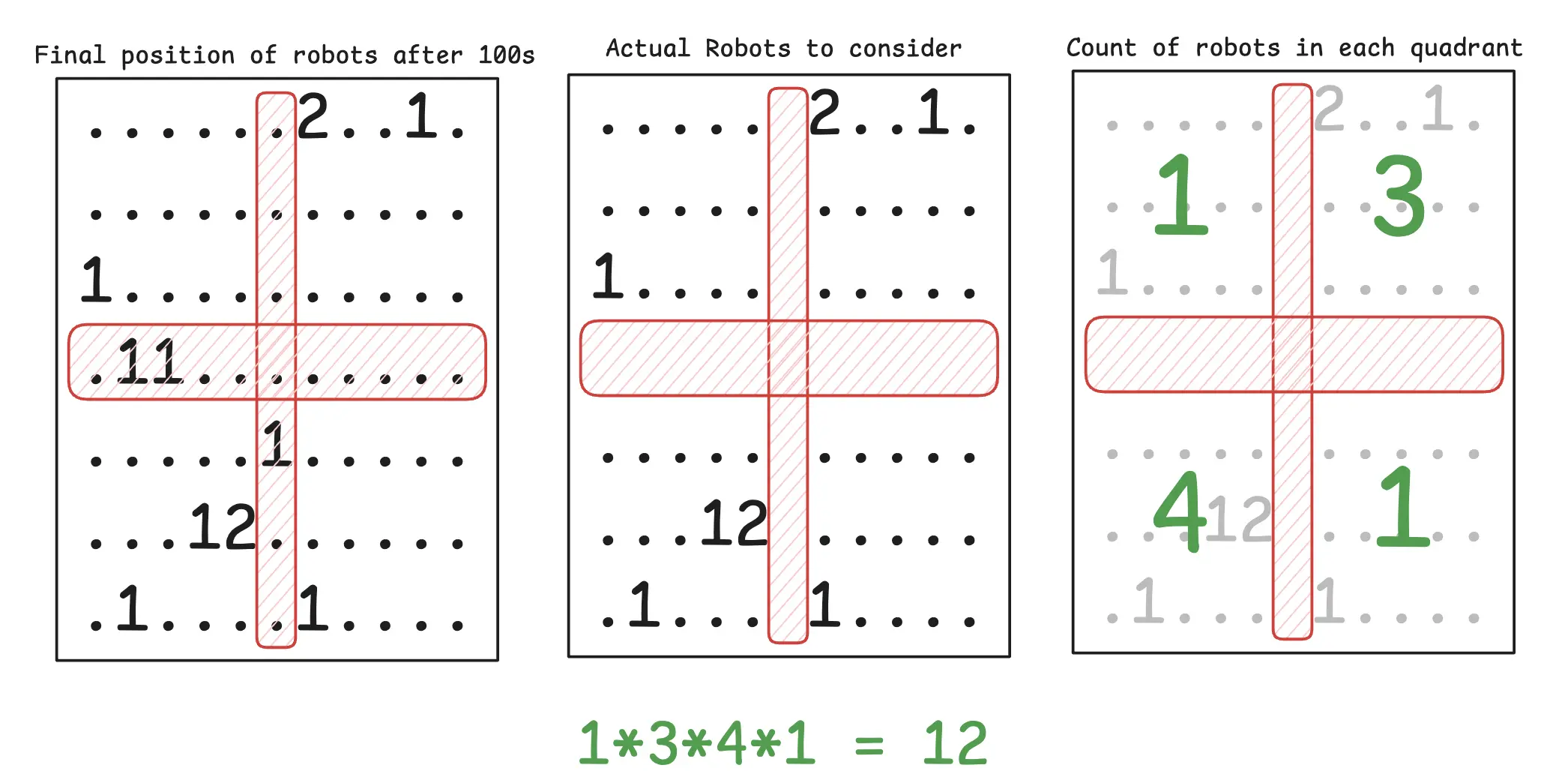
We need to find the position of all robots after 100 seconds. Once we have the final positions of robots, we need to find the count of robots in each quadrant ignoring the middle row and column. The final answer should be the product of count of robots in each quadrant.

Solution

This is a fairly simple problem. To find the position of a given robot after X seconds:

1. We simply multiply X into the velocity.
2. Since robots are restricted to move in a space of 101 tiles wide and 103 tiles tall, to get the actual position, we will have to be careful.

Implementing this:

func getPositionAfterCountSeconds(r robot, count int, maxX, maxY int) aoc.Coordinates {
	x, y := r.position.X, r.position.Y

	a := (x + count*r.velocity.X) % maxX
	b := (y - count*r.velocity.Y) % maxY

	if a >= maxX {
		a = a - maxX
	}

	if a < 0 {
		a = maxX + a
	}

	if b <= -maxY {
		b = b + maxY
	}

	if b > 0 {
		b = -(maxY - b)
	}
	return aoc.Coordinates{a, b}
}

Now we just need to calculate number of robots in each quadrant. Here we need to be careful to ignore the robots that land on the middle row and column.

func getScore(r []robot, maxX, maxY int) int {
	quad := []int{0, 0, 0, 0}
	for _, ro := range r {
		newPosition := getPositionAfterCountSeconds(ro, 100, maxX, maxY)
		x, y := newPosition.X, newPosition.Y
		switch {
		case x < maxX/2 && y > -maxY/2:
			quad[0] += 1
		case x > maxX/2 && y > -maxY/2:
			quad[1] += 1
		case x < maxX/2 && y < -maxY/2:
			quad[2] += 1
		case x > maxX/2 && y < -maxY/2:
			quad[3] += 1
		}
	}
	return quad[0] * quad[1] * quad[2] * quad[3]
}

And that’s it! The value returned by the above function is the answer for part one.

Part 2

Now this is where things get a little tricky. We now need to find the number of seconds after the robots arrange themselves into a Christmas tree.

Solution

Sine we don’t know how the Christmas tree looked like, I initially didn’t have any clue how to go about it.

Approach 1

I started with printing out the grid for the first 100000 iterations to a file and manually find if any of the iterations had an image by searching for 10 # continuously.

Simple functions that get the position of robots after every second, create a grid where # represent the position of robots and . signify empty spaces and finally printing this grid to the file.

func writeGridAfterXSecond(r []robot, maxX, maxY int, count int) {
	grid := make([][]string, maxY)
	for i := 0; i < maxY; i++ {
		grid[i] = strings.Split(strings.Repeat(".", maxX), "")
	}
	for _, ro := range r {
		newLoc := getPositionAfterCountSeconds(ro, count, maxX, maxY)
		grid[-newLoc.Y][newLoc.X] = "#"
	}
	printGrid(grid, maxX, maxY)
	return
}

func printGrid(grid [][]string, maxX, maxY int) {
	for i := 0; i < maxY; i++ {
		aoc.WriteToFile("output.txt", fmt.Sprintf(strings.Join(grid[i], "")+"\n"))
	}
}

func printAllPossibleGridsToFile(r []robot, maxX, maxY int) {
	count := 0
	for count < 103*101 {
		writeGridAfterXSecond(r, maxX, maxY, count)
		aoc.WriteToFile("output.txt", fmt.Sprintf("output after %d seconds\n", count))
		count++
	}
}

Grepping the file, I was able to find the answer. But how do we do this programatically?

Approach 2

Above is a brute force + manual effort. How can we do this programmatically? What if the image would have been something else? The problem boils down to, how to look for an image (any image) in a 2D grid.

After looking at a few people’s solution, I learned that the entropy of an image is low as compared to a random distribution of pixels.

Applying this to our usecase, the entropy of arrangement of robots in the grid should be lowest when they form an image, in our case a Christmas Tree. Someone visualised how starkly low the entropy would be as opposed to other frames!

We can calculate the entropy of a 2D grid using Shannon’s Entropy. Implementing Shannon’s Entropy:

// Entropy calculates the entropy of a 2D grid
// using Shannon's Entropy.
// https://en.wikipedia.org/wiki/Entropy_(information_theory)
func Entropy(img [][]int) float64 {
	// Flatten the image into a single slice
	var flatImg []int
	for _, row := range img {
		flatImg = append(flatImg, row...)
	}

	// Calculate histogram with 256 bins
	bins := 256
	histogram := make([]float64, bins)
	for _, value := range flatImg {
		if value >= 0 && value < bins {
			histogram[value]++
		}
	}

	// Normalize histogram
	totalPixels := float64(len(flatImg))
	for i := range histogram {
		histogram[i] /= totalPixels
	}

	// Filter out zero probabilities
	var marg []float64
	for _, prob := range histogram {
		if prob > 0 {
			marg = append(marg, prob)
		}
	}

	// Calculate entropy
	entropy := 0.0
	for _, p := range marg {
		entropy -= p * math.Log2(p)
	}

	return entropy
}

Now, we can iterate over 103*101 seconds and find the second with the lowest entropy. Printing the arrangement of robots at this second, we can see the Christmas Tree!

The above method is generalised and can be used to detect any image formed by the robots. Someone came up with an input that arranges the robots in a QR code! You can find the input here. Solve it for a nice festive delight :)

Today’s Part 2 started out quite vague but I ended up learning a tonne from checking out how different people solved this in such unique ways! Some folks found out the result by finding the second with the least size of compressed grid, others used their file explorer, someone also figured out how to use part 1 to solve part2, and ofcourse there were folks who used Chinese Remainder Theorem. All in all, a fun day!

How did you solve Day 14? I would love to compare notes and checkout your solution. Reach out to me on Twitter, Bluesky or on e-mail at contact[at]shraddhaag[dot]dev.