Advent of Code Day 15 was one I spend quite a lot of time with a pen and paper figuring out all the corner cases to solve part two only to realise a much simpler solution later on. Let’s figure out how to solve this very interesting puzzle.

---

The below is a guest post by the amazing Shraddha Agrawal.

---

Part 1

Input is the map of the area we need to navigate followed by the order of movements we (a robot) attempt to make. The map has four types of tiles:

1. . - the tile is empty.
2. O - the tile represents a box.
3. # - the tile is a wall.
4. @ - our current position.

The rules for following the given list of movements:

1. If we encounter a coordinate which contains a box, ie a O tile, we attempt to push the box and all consecutive boxes till there is space to accommodate the current move. A box can not be moved on a coordinate containing a wall, ie a # tile.
2. If moving boxes is not possible, the current move is ignored and we do not change our position.

An example of applying the above rules looks like this:

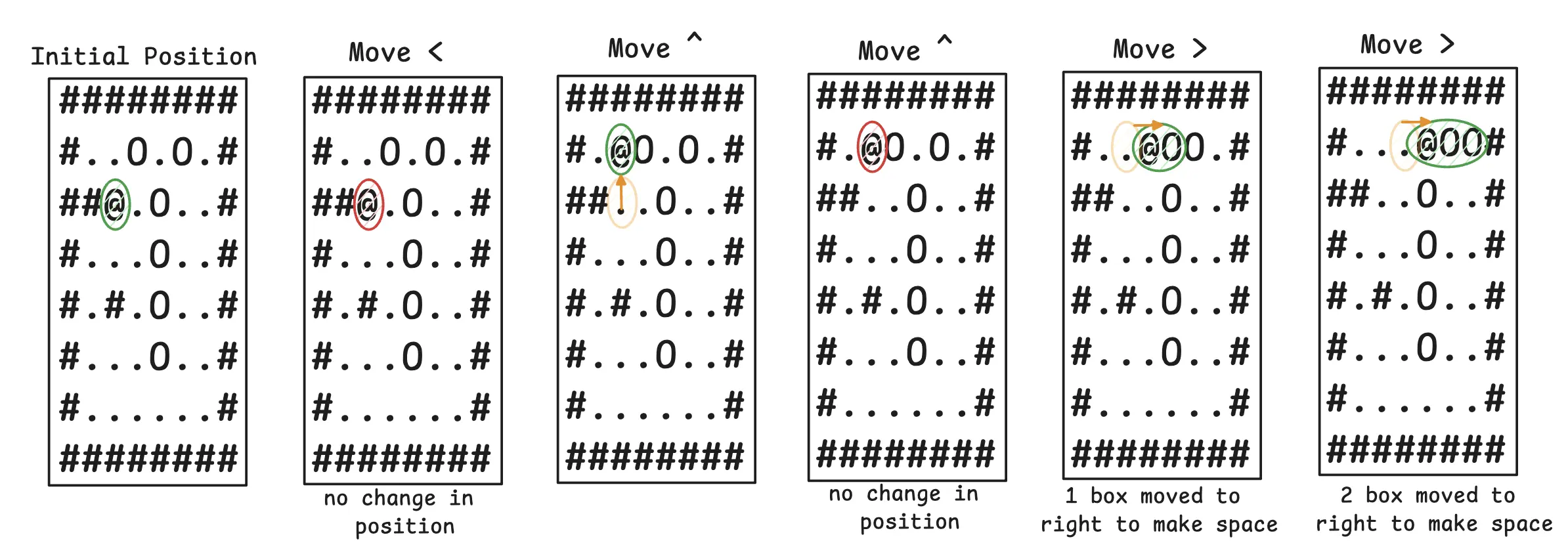
For part one, we need to calculate the final position of the boxes in the map after all given movement steps have been processed. Once done, the final answer should be the sum of Y coordinates of all boxes and the sum of X coordinates of all boxes multiplied by 100.

Solution

Implementing this is fairly simple. For each given direction, we need to check the current state of the map and see if a movement is possible. For . and # the answer is a simple yes and no respectively. For handling O tile, ie a block, in a loop till we hit a wall, I checked if the next position in the desired direction is an empty tile, ie .. If yes, we can move all boxes in the given direction by 1. Doing this efficiently, I replaced the empty tile with a box and moved our current position in the desired direction.

I used a switch statement for this. The function to return the grid after processing a single step looks like this:

func processStep(start aoc.Coordinates, grid [][]string, step string) ([][]string, aoc.Coordinates) {
	var direction aoc.Coordinates
	switch step {
	case "^":
		direction = aoc.Coordinates{0, -1}
	case "<":
		direction = aoc.Coordinates{-1, 0}
	case ">":
		direction = aoc.Coordinates{1, 0}

	case "v":
		direction = aoc.Coordinates{0, 1}
	}

	newX, newY := start.X+direction.X, start.Y+direction.Y

	if !isValidStep(aoc.Coordinates{newX, newY}, grid) {
		return grid, start
	}

	switch grid[newY][newX] {
	case ".":
		grid[start.Y][start.X] = "."
		grid[newY][newX] = "@"
		return grid, aoc.Coordinates{newX, newY}
	case "#":
		return grid, start
	case "O":
		for isValidStep(aoc.Coordinates{newX, newY}, grid) {
			switch grid[newY][newX] {
			case ".":
				grid[start.Y][start.X] = "."
				grid[newY][newX] = "O"
				grid[start.Y+direction.Y][start.X+direction.X] = "@"
				return grid, aoc.Coordinates{start.X + direction.X, start.Y + direction.Y}
			case "#":
				return grid, start
			}
			newX += direction.X
			newY += direction.Y
		}
	}
	return grid, start
}

Calling the above function for all directions given in the input on the initial gird with the starting position of the robot, we can find the final position of the boxes.

func getFinalGrid(grid [][]string, movements string, start aoc.Coordinates) int {
	for _, char := range movements {
		grid, start = processStep(start, grid, string(char))
	}

	count := 0
	for j, row := range grid {
		for i, char := range row {
			switch char {
			case "O", "[":
				count += (i) + (j)*100
			}
		}
	}
	return count
}

This gives us the answer for part 1. Now, lets move on to the more interesting part 2.

Part 2

Now, we need to expand the input layout of the warehouse. The rules of expansion are:

• a single # turns into ##.
• a singe O turns into [].
• a single . turns into ...
• a single @ turns into @..

Doing this for the following sample input would result in the following expanded grid:

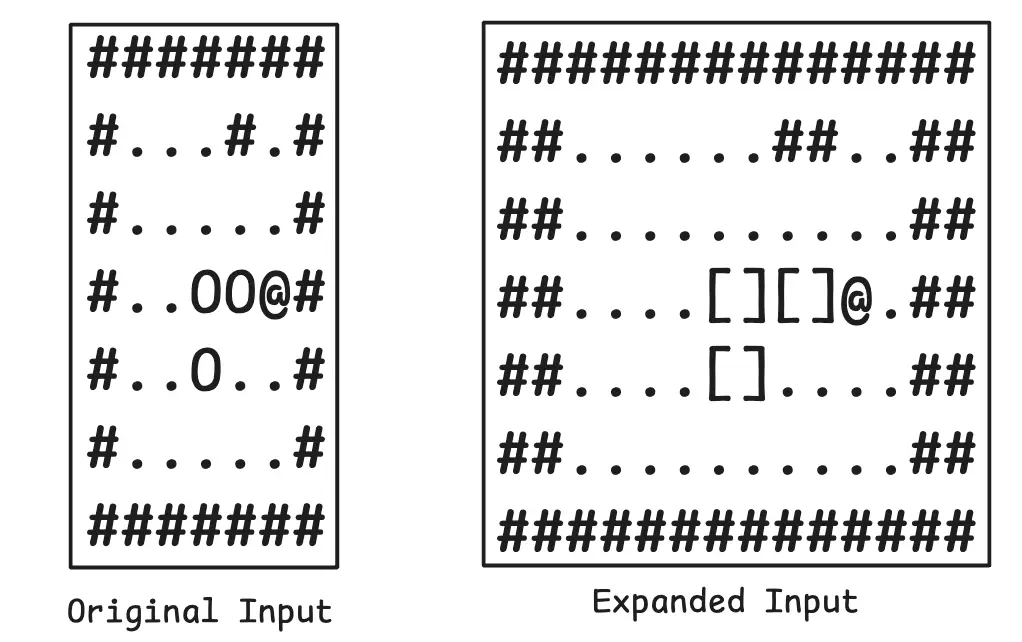
Applying the moving rules to the above grid would look like this:

Again, like part one, we need to calculate the sum of final Y coordinates of all boxes and the sum of final X coordinates of all boxes multiplied by 100.

Solution

First, lets expand the input grid given the new rules:

func expandGrid(input [][]string) (finalGrid [][]string, start aoc.Coordinates) {
	for j, row := range input {
		finalRow := []string{}
		for i, char := range row {
			switch char {
			case ".":
				finalRow = append(finalRow, []string{".", "."}...)
			case "#":
				finalRow = append(finalRow, []string{"#", "#"}...)
			case "O":
				finalRow = append(finalRow, []string{"[", "]"}...)
			case "@":
				start.X = i * 2
				start.Y = j
				finalRow = append(finalRow, []string{"@", "."}...)
			}

		}
		finalGrid = append(finalGrid, finalRow)
	}
	return finalGrid, start
}

Now, the main change from the previous part is:

1. Boxes are created by 2 cells instead of just 1.
2. If a box can be moved and if yes, how many boxes to move isn’t as straight forward anymore.

The main crux of the problem is to figure out if a box can move or not. If yes, then how many boxes to move.

A box can move:

• horizontally if we encounter an empty tile when we keep moving in the desired direction that is blocked by boxes before encountering a wall. This is similar to how we were determining if a box can be moved in part one.
• vertically, is a bit more challenging. This is similar to a pile of gift boxes, we can move only if we can move all gift boxes resting on top (or below) the main gift box to move. Similarly, for a tree of connected boxes, if the child nodes all have empty spaces after them then the original box can be moved.

If a box is moveable, which boxes to move?

• horizontally - this is pretty straightforward like before. One by one we can move all boxes by 1 tile towards the empty space found till we create an empty space for us to move.
• vertically - this is what took me a lot of time to figure out, which in hindsight its quite simple. all the boxes that are connected to each other and form the “tree of connected boxes” are the ones to move. In other words, all the boxes we checked above to ensure a box can be moved, are also the boxes that need to be moved.

For moving boxes vertically, I found it was easiest to first move the child nodes to the empty spaces found and then move the rest of the boxes iteratively. When a box is moved, we replace it with an empty tile. When we are done moving all the boxes, we will be left with an empty space for us to occupy. Doing it this way we can skip checking for all the corner cases to figure out what to replace the box with when it is moved as it will automatically be taken care of.

I implemented the function to move boxes using a recursive DFS function:

// moveBoxesHorizontally does a DFS to look for the first empty slot where all the
// blocks can be shifted.
func moveBoxesHorizontally(start, direction aoc.Coordinates, grid [][]string) bool {
	newX, newY := start.X+direction.X, start.Y+direction.Y

	switch grid[newY][newX] {
	case "#":
		return false
	case ".":
		grid[newY][newX], grid[start.Y][start.X] = grid[start.Y][start.X], grid[newY][newX]
		return true
	case "]", "[":
		isPossible := moveBoxesHorizontally(aoc.Coordinates{newX, newY}, direction, grid)
		if !isPossible {
			return false
		}
		grid[start.Y][start.X], grid[newY][newX] = grid[newY][newX], grid[start.Y][start.X]
	}
	return true
}

And I used a BFS function to first check if a box can be moved. When checking this, I saved the boxes I checked in a slice. If the box can be moved, we iterate over the slice starting from the end of the slice to move all the boxes.

// moveBoxVertically does a BFS to check if all child nodes end with a free space
// such that boxes can be moved. If true, we move the boxes vertically in the given
// direction.
func moveBoxVertically(start, direction aoc.Coordinates, grid [][]string) bool {
	next := []aoc.Coordinates{start}
	if grid[start.Y][start.X] == "]" {
		next = append(next, aoc.Coordinates{start.X - 1, start.Y})
	} else {
		next = append(next, aoc.Coordinates{start.X + 1, start.Y})
	}

	visited := make(map[aoc.Coordinates]struct{})
	visitedSlice := []aoc.Coordinates{}

	for len(next) != 0 {
		process := next[0]
		next = next[1:]

		if _, ok := visited[process]; ok {
			continue
		}

		visited[process] = struct{}{}
		visitedSlice = append(visitedSlice, process)

		newX, newY := process.X+direction.X, process.Y+direction.Y
		switch grid[newY][newX] {
		case ".":
			continue
		case "#":
			return false
		case "]":
			next = append(next, aoc.Coordinates{newX, newY})
			next = append(next, aoc.Coordinates{newX - 1, newY})
		case "[":
			next = append(next, aoc.Coordinates{newX, newY})
			next = append(next, aoc.Coordinates{newX + 1, newY})
		}
	}

	// When traversing the grid to perfrom BFS, we also store all the cells
	// that we are processing, as these will be the same cells that will need to be moved.
	// We start shifting cells from the end of the traversed path
	// so that we first move the top-most/bottom-most cell first.
	// Each cell is shifted in the desired direction and the current cell is marked empty.
	// Moving blocks this way saves us from a lot of corner cases.
	for i := len(visitedSlice) - 1; i >= 0; i-- {
		x, y := visitedSlice[i].X+direction.X, visitedSlice[i].Y+direction.Y
		grid[y][x] = grid[visitedSlice[i].Y][visitedSlice[i].X]
		grid[visitedSlice[i].Y][visitedSlice[i].X] = "."
	}

	return true
}

Now all we need to do is call these above functions in our original processStep function. And with that we can iteratively process all input movements to find the final position of all boxes to find the answer to art 2. You can find my final code here.

This day was quite a challenging one, especially figuring out how to move the boxes vertically. In hindsight it was quite straightforward when thinking about it as a tree, which isn’t my strongest data structure. When I finally saw the boxes move just right was quite a nice feeling!

How did you solve Day 15? I would love to compare notes and checkout your solution. Reach out to me on Twitter, Bluesky or on e-mail at contact[at]shraddhaag[dot]dev.