With Advent of Code Day 18 the infamous 2D grid returns. Let’s figure it out!

---

The below is a guest post by the amazing Shraddha Agrawal.

---

Part 1

Input is a list of coordinates of walls that fall each second on an area that is 71 tiles wide and 71 tiles tall. We need to get the grid after 1024 walls have fallen.

Consider the following area which is 7 tile wide and 7 tile tall. Here is how the grid looks like after each second as the walls keep falling.

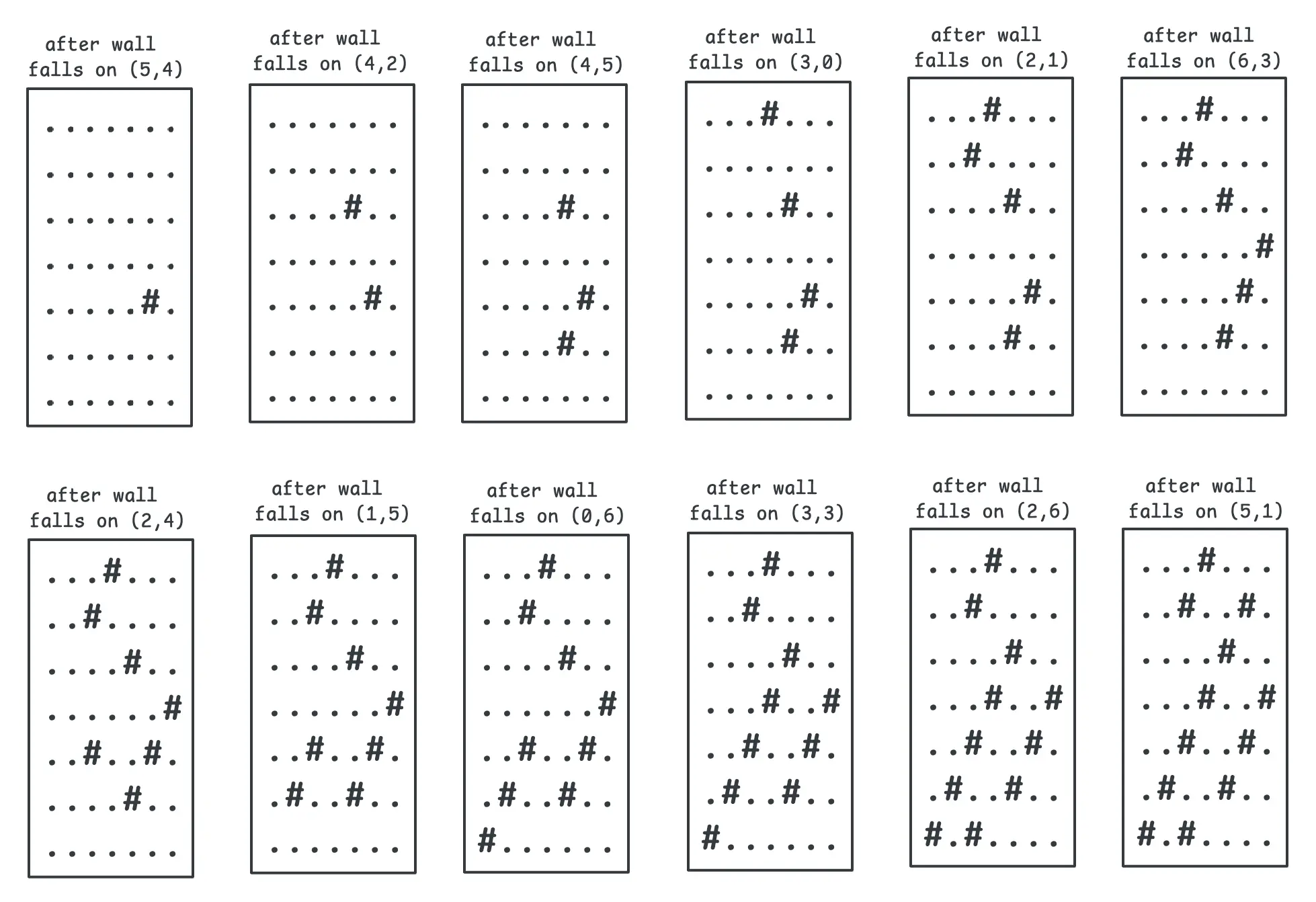
Our current position is at coordinates (0,0) and we need to reach 70,70 to exit the grid. In the grid after 1024 walls have fallen, we need to find the number of steps in the shortest path possible from (0,0) to (70,70). We can go in any direction, the only restriction is that we can not step on a wall.

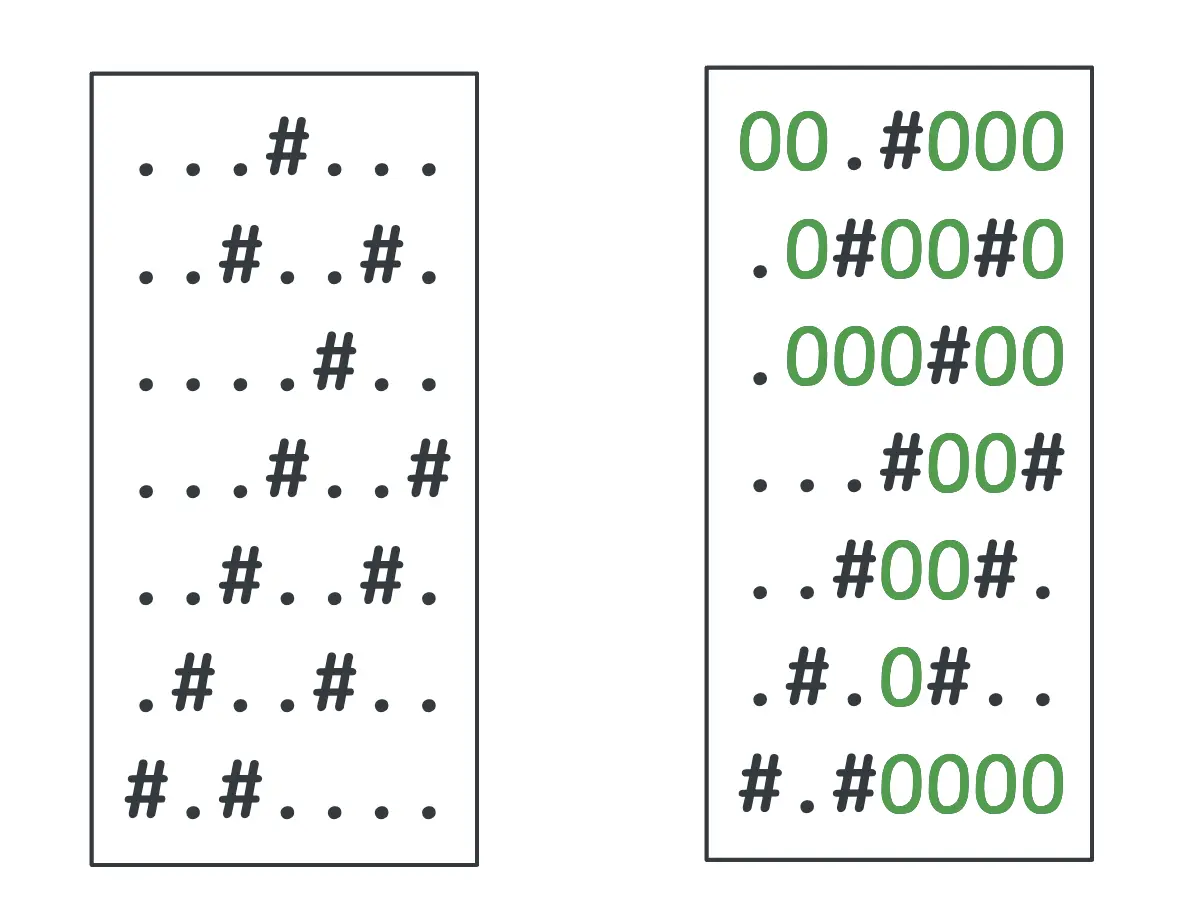
In the above example, after 12 seconds, the shortest path to the exit consists of 22 steps, visualised below.

Solution

To get the grid after 1024 seconds, we just need to process the first 1024 walls on an empty grid. I kept the number of lines to process variable as that might be required for part 2. This can be done like below:

func createGrid(input []string, maxX, maxY int, linesToProcess int) [][]string {
	grid := make([][]string, maxY)
	for index, _ := range grid {
		resultString := strings.Repeat(".", maxX)

		grid[index] = strings.Split(resultString, "")
	}

	for _, row := range input[:linesToProcess] {
		nums := aoc.FetchSliceOfIntsInString(row)
		grid[nums[1]][nums[0]] = "#"
	}

	return grid
}

Then since we need to find the shortest path, we’ll use Dijkstra’s algorithm. It’s very similar to how we implemented it for Day 16, the only difference being now we can go in all 4 directions next instead of a limited 90 degree turn. This will give us the answer for part 1.

Part 2

Now we need to find the very first coordinates from the falling walls, that will block off the path to exit.

Solution

Since we already know that after 1024 walls falling we still have a path to exit, we can start our search from there.

Now a naive way to solve this would be for each new wall, we add it to the grid and then check with Dijkstra’s algorithm if a path still exists. While this might work, lets figure out a way to optimise this.

Let’s suppose we already have a path from (0,0) to (70,70) (we already found this in part 1). Now for every new wall falling, the path will only change if the wall is falling on the path. If the wall lands on a tile which is not part of the path to exit, we still have a valid way to exit the grid. In such cases, there is no need to check with Dijkstra’s if a path still exists. When the wall does fall on the path, we check with Dijkstra’s. If a valid path exists, we update the path to this new one and use this new path to check the following falling walls against.

Implementing this is simple enough:

func getCount(input []string, start, maxX, maxY int, originalPath map[aoc.Coordinates]int) string {
	for i := start; i < len(input); i++ {

		// if the new block does not land on the previous path,
		// it will not block the path and hence, a valid path exists.
		newObstacleCo := aoc.Coordinates{aoc.FetchSliceOfIntsInString(input[i-1])[0], aoc.FetchSliceOfIntsInString(input[i-1])[1]}
		if _, ok := originalPath[newObstacleCo]; !ok {
			continue
		}

		grid := createGrid(input, maxX, maxY, i)
		count, path := dijktras(grid)
		if count == -1 {
			return input[i-1]
		}
		originalPath = path
	}
	return "none"
}

And this gives us the answer to Part 2! You can find my final code here.

This was a quite neat little problem, especially part two. It was fun to find the optimisation to fasten the runtime. I expected a much more difficult part two where we might have to handle time as well, as we are walking through the maze but I’ll take an easy day!

How did you solve Day 18? I would love to compare notes and checkout your solution. Reach out to me on Twitter, Bluesky or on e-mail at contact[at]shraddhaag[dot]dev.