Advent of Code Day 21 was touuuugh! I got stuck with the first part itself for a long time before I figured it out and then part 2 took its own sweet time. Let’s figure it out!

---

The below is a guest post by the amazing Shraddha Agrawal.

---

Part 1

We are given a series of keycodes to press on a numeric keypad. But we can not access the numeric key pad ourselves. Instead a robot can press the keys on the numeric keypad. The robot is controlled using a directional keypad. There are 2 layers of robots between us and the alphabetical keypad. The layout looks like:

1. One directional keypad that we are using.
2. Two directional keypads that robots are using.
3. One numeric keypad (on a door) that a robot is using.

The numeric keypad and the directional keypad are laid out like below, where the empty space is illegal to traverse.

Rule for pressing keys on both the keypads:

1. To register a key on the keypad, we need to press the A key after completing the sequence to get the robot in the right position.
2. We can not traverse over the blank key in both the keypads.
3. The inital position of robot at each keypad is A.

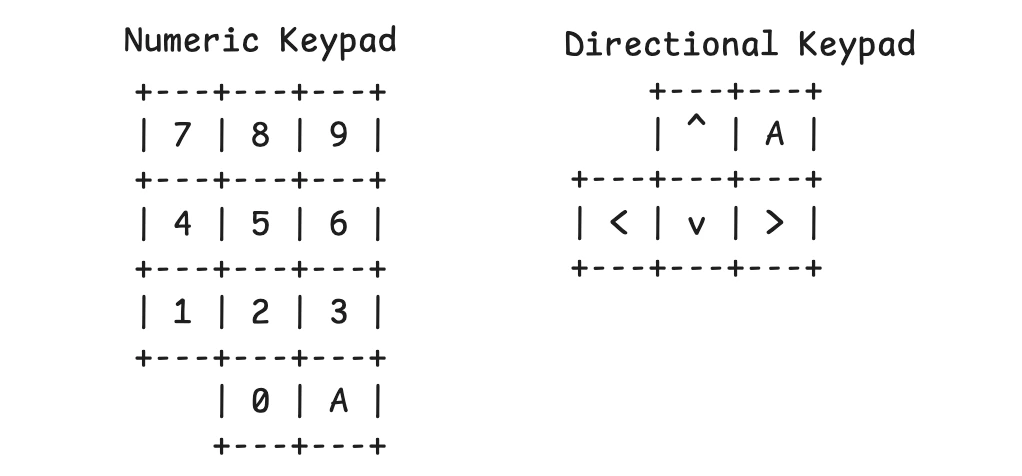
Consider the example keycode, 029A. To press this on the numeric keypad, the following keys will need to be pressed by robots and us.

We need to find the shortest number of presses for each input keycode. The final answer should be the sum of the product of the length of the sequence for each code with the numeric part of the code.

Solution

Let’s start off with representing both the keypads with coordinates. I did this like below:

The boxes in red are illegal to traverse. I hardcoded these values in a map for each of the keypads:

	numericalMap := make(map[string]aoc.Coordinates)
	numericalMap["A"] = aoc.Coordinates{2, 0}
	numericalMap["0"] = aoc.Coordinates{1, 0}
	numericalMap["1"] = aoc.Coordinates{0, 1}
	numericalMap["2"] = aoc.Coordinates{1, 1}
	numericalMap["3"] = aoc.Coordinates{2, 1}
	numericalMap["4"] = aoc.Coordinates{0, 2}
	numericalMap["5"] = aoc.Coordinates{1, 2}
	numericalMap["6"] = aoc.Coordinates{2, 2}
	numericalMap["7"] = aoc.Coordinates{0, 3}
	numericalMap["8"] = aoc.Coordinates{1, 3}
	numericalMap["9"] = aoc.Coordinates{2, 3}

	directionalMap := make(map[string]aoc.Coordinates)
	directionalMap["A"] = aoc.Coordinates{2, 1}
	directionalMap["^"] = aoc.Coordinates{1, 1}
	directionalMap["<"] = aoc.Coordinates{0, 0}
	directionalMap["v"] = aoc.Coordinates{1, 0}
	directionalMap[">"] = aoc.Coordinates{2, 0}

Now, the struggle starts, bear with me.

For some reason I assumed that there is only one length of the final sequence of button presses for each code irrespective of the order in which we press the buttons. But I was quickly proven wrong and spend a frustrating amount of time trying to understand why. The only good thing was I got stuck with the test input itself so I didn’t have to waste time trying to find the keycode that was causing problem in the actual puzzle input. Here is a simple explanation why the final sequences can be of different length depending on the path we take.

First, a few clarifications:

1. We should absolutely not take a path which traverses over the illegal coordinate. This is (0,0) for the numeric keypad and (0,1) for the directional keypad.
2. Taking the least amount of turns takes highest precedence for getting shorter subsequence. This is true because when we have less turns in the initial sequence, we will spend less time in intermediate robots trying to create that subsequence with directional keypad.
3. Repetition is the same direction is beneficial as that translates to clicking A multiple times on intermediate robots.

From the above points, we essentially need to figure out whether we should traverse horizontal or vertical first.

Now, lets see what are the different ways to press 7 after 3 and to press v after A.

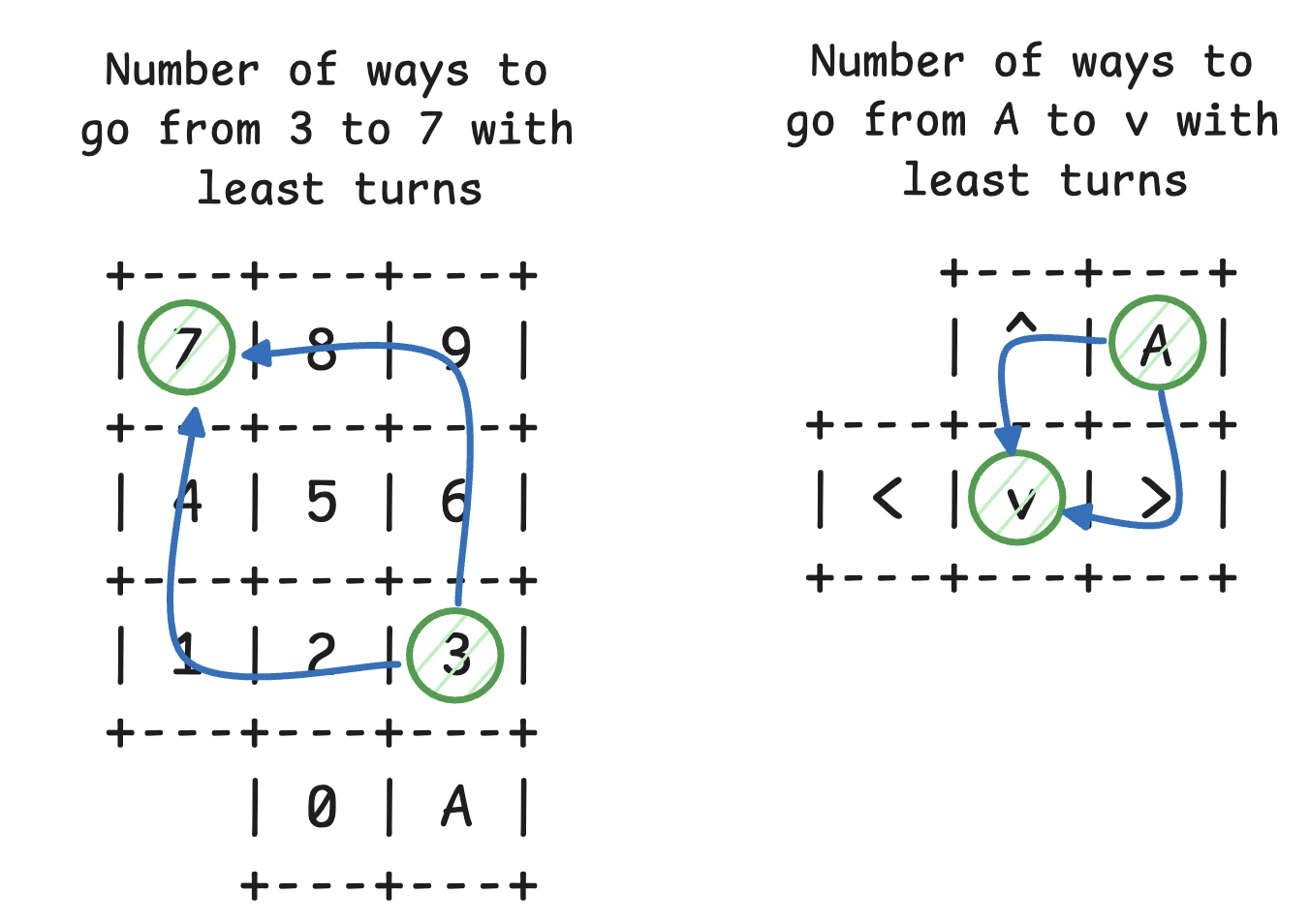
As we can see, there are two different ways to press both combinations. (I have not visualised the paths with more turns as that we have already established that is a less efficient way of pressing buttons.)

Depending on which way we take from the above examples, the length of the final subsequence will change. After a lot (trust me, a LOT) of trail error, I landed on the final conclusion for precedence order:

1. Prefer the path with the least turns.
2. If multiple paths with least turns are available, then preference order is Left > Up > Down > Right.

I couldn’t really understand why the above works as this was derived from trail and error, but a great explanation can be found here.

Implementing the above rules for numeric keypad we get the following:

func getPressesForNumericPad(input []string, start string, numericalMap map[string]aoc.Coordinates) []string {
	current := numericalMap[start]
	output := []string{}

	for _, char := range input {
		dest := numericalMap[char]
		diffX, diffY := dest.X-current.X, dest.Y-current.Y

		horizontal, vertical := []string{}, []string{}

		for i := 0; i < aoc.Abs(diffX); i++ {
			if diffX >= 0 {
				horizontal = append(horizontal, ">")
			} else {
				horizontal = append(horizontal, "<")
			}
		}

		for i := 0; i < aoc.Abs(diffY); i++ {
			if diffY >= 0 {
				vertical = append(vertical, "^")
			} else {
				vertical = append(vertical, "v")
			}
		}

		// prioritisation order:
		// 1. moving with least turns
		// 2. moving < over ^ over v over >

		if current.Y == 0 && dest.X == 0 {
			output = append(output, vertical...)
			output = append(output, horizontal...)
		} else if current.X == 0 && dest.Y == 0 {
			output = append(output, horizontal...)
			output = append(output, vertical...)
		} else if diffX < 0 {
			output = append(output, horizontal...)
			output = append(output, vertical...)
		} else if diffX >= 0 {
			output = append(output, vertical...)
			output = append(output, horizontal...)
		}

		current = dest
		output = append(output, "A")
	}
	return output
}

And similarly for directional keypad:

func getPressesForDirectionalPad(input []string, start string, directionlMap map[string]aoc.Coordinates) []string {
	current := directionlMap[start]
	output := []string{}

	for _, char := range input {
		dest := directionlMap[char]
		diffX, diffY := dest.X-current.X, dest.Y-current.Y

		horizontal, vertical := []string{}, []string{}

		for i := 0; i < aoc.Abs(diffX); i++ {
			if diffX >= 0 {
				horizontal = append(horizontal, ">")
			} else {
				horizontal = append(horizontal, "<")
			}
		}

		for i := 0; i < aoc.Abs(diffY); i++ {
			if diffY >= 0 {
				vertical = append(vertical, "^")
			} else {
				vertical = append(vertical, "v")
			}
		}

		// prioritisation order:
		// 1. moving with least turns
		// 2. moving < over ^ over v over >

		if current.X == 0 && dest.Y == 1 {
			output = append(output, horizontal...)
			output = append(output, vertical...)
		} else if current.Y == 1 && dest.X == 0 {
			output = append(output, vertical...)
			output = append(output, horizontal...)
		} else if diffX < 0 {
			output = append(output, horizontal...)
			output = append(output, vertical...)
		} else if diffX >= 0 {
			output = append(output, vertical...)
			output = append(output, horizontal...)
		}
		current = dest
		output = append(output, "A")
	}
	return output
}

Now, to solve part 1, we just need to call the above functions in the order of robots operating on the keypads to find the answer:

func getSequence(input []string, numericalMap, directionalMap map[string]aoc.Coordinates) int {
	count := 0
	for _, line := range input {
		row := strings.Split(line, "")
		seq1 := getPressesForNumericPad(row, "A", numericalMap)
		seq2 := getPressesForDirectionalPad(seq1, "A", directionalMap)
		seq2 = getPressesForDirectionalPad(seq2, "A", directionalMap)
		count += aoc.FetchNumFromStringIgnoringNonNumeric(line) * len(seq2)
	}
	return count
}

And that gives us the answer for part 1! That was tough but there is still part two to solve.

Part 2

Now instead of 2 intermediate robots, we have 25. So the new layout looks like:

1. One directional keypad that we are using.
2. 25 directional keypads that robots are using.
3. One numeric keypad (on a door) that a robot is using.

Again, the answer will be the sum of the product of the length of the sequence for each code with the numeric part of the code.

Solution

By simply updating the getSequence function to call the getPressesForDirectionalPad 25 times obviously did not cut it as the runtime got out of hand. So now we will need to optimise it, there must be some computation we can save!

While I was debugging the above, I realised that for directional keypad, each button sequence starts at A and ends at A. We can use this to divide the sequence obtained by intermediate robots into individual sections and process them independently.

Now that we have a small enough key to work with, we can also make use of memoisation. We can create a map and store the length of sequence for each key after each robot is done processing. That is, we will use a string key and the value will be an int slice of length 25. This will help us limit the number of computation we need to make. This is similar to Day 11 where instead of storing the sequence of all stone, we just stored the count after each blink.

Writing a recursive solution for this would look like:

func getCountAfterRobots(input []string, maxRobots int, robot int, cache map[string][]int, directionalMap map[string]aoc.Coordinates) int {
	if val, ok := cache[strings.Join(input, "")]; ok {
		if val[robot-1] != 0 {
			return val[robot-1]
		}
	} else {
		cache[strings.Join(input, "")] = make([]int, maxRobots)
	}

	seq := getPressesForDirectionalPad(input, "A", directionalMap)
	cache[strings.Join(input, "")][0] = len(seq)

	if robot == maxRobots {
		return len(seq)
	}

	splitSeq := getIndividualSteps(seq)

	count := 0
	for _, s := range splitSeq {
		c := getCountAfterRobots(s, maxRobots, robot+1, cache, directionalMap)
		if _, ok := cache[strings.Join(s, "")]; !ok {
			cache[strings.Join(s, "")] = make([]int, maxRobots)
		}
		cache[strings.Join(s, "")][0] = c
		count += c
	}

	cache[strings.Join(input, "")][robot-1] = count
	return count
}

Now we just need to call this function, after getting the sequence from the numeric keypad. Altering getSequence function, we finally have:

func getSequence(input []string, numericalMap, directionalMap map[string]aoc.Coordinates, robots int) int {
	count := 0
	cache := make(map[string][]int)
	for _, line := range input {
		row := strings.Split(line, "")
		seq1 := getPressesForNumericPad(row, "A", numericalMap)
		num := getCountAfterRobots(seq1, robots, 1, cache, directionalMap)
		count += aoc.FetchNumFromStringIgnoringNonNumeric(line) * num
	}
	return count
}

And that is the answer for part two. You can find my final code here.

This was a tough day, for both part 1 and 2. Spotting patterns, dynamic programming and memoisation, all came to play. Apart from this, there were small things that had to be kept in mind to arrive at the final solution. This took me a long time to get the final answer, I’m glad this puzzle was on a weekend! All that said, it was quite a fun puzzle to solve, and reminded me of Day 10 last year.

How did you solve Day 21? I would love to compare notes and checkout your solution. Reach out to me on Twitter, Bluesky or on e-mail at contact[at]shraddhaag[dot]dev.