Advent of Code, Day 5 was interesting. Hidden in there was a custom sort, lets dig it out!

---

The below is a guest post by the amazing Shraddha Agrawal.

---

Part 1

The problem is posed as printing updates for an instruction manual. The input had two sections:

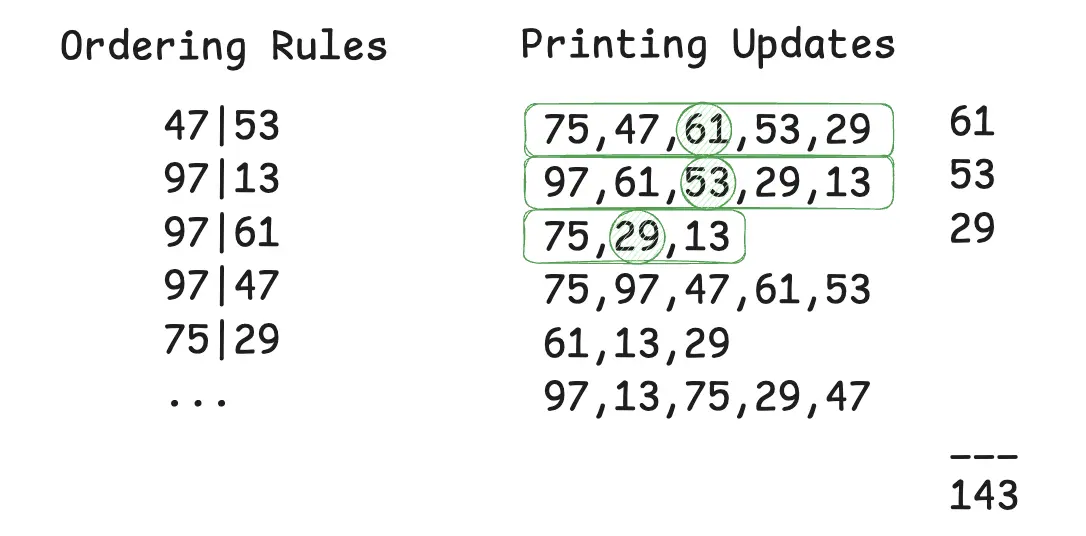
1. Ordering Rules: Rows of numbers where each row is in the format X|Y, X and Y signify page numbers. Each row is a rule, such that X should be printed before Y.
2. Updates: Each row in this section is an array of numbers, signifying the order in which pages are printed. This row may be valid or invalid.

For the first part, we need to validate the updates in second section as per the ordering rules in the first section. Final answer should be the sum of middle value of all valid updates.

Solution

First, we need to have the ordering rules in a handy data structure so we can easily use it to validate an update. I went with a Golang map here, with an int key and a slice of ints for its value such that in a valid printing update, the key should come before all the numbers in the value slice.

func getRulesMap(rules [][]int) map[int][]int {
	ruleMap := make(map[int][]int)

	for _, rule := range rules {
		if _, ok := ruleMap[rule[0]]; ok {
			ruleMap[rule[0]] = append(ruleMap[rule[0]], rule[1])
		} else {
			ruleMap[rule[0]] = []int{rule[1]}
		}
	}
	return ruleMap
}

Now, how do we validate an update? The key idea I am using to solve part 1 is that, for each number in a valid update, all numbers after the current number should exist in the value slice for the current number’s key in the rules map we created above. If any of the subsequent numbers don’t exist in the value slice, it means the update is violating the rules. Code for implementing this:

func isValidUpdate(ruleMap map[int][]int, update []int) bool {
	for i := 0; i < len(update)-1; i++ {
		if _, ok := ruleMap[update[i]]; !ok {
			return false
		}
		for j := i + 1; j < len(update); j++ {
			found := false
			for _, element := range ruleMap[update[i]] {
				if element == update[j] {
					found = true
					break
				}
			}
			if !found {
				return false
			}
		}
	}
	return true
}

Now that we have both of these pieces in place, we just need to get the sum of middle number of all valid updates to get the final answer. You can find code for this here.

Part 2

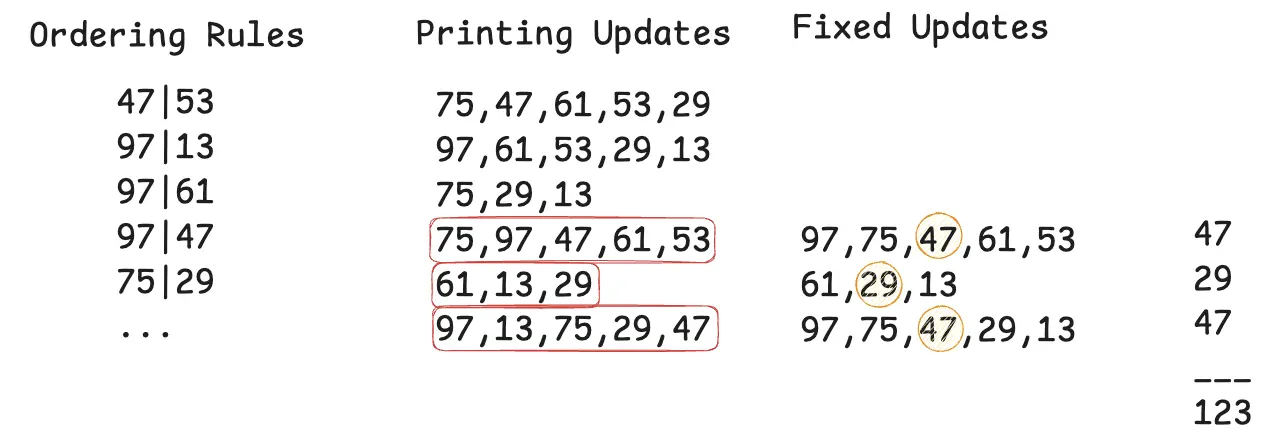
Now comes the interesting bit. For the second part, we had to fix all the invalid updates. The valid answer will be the sum of middle number of the fixed updates.

Solution

Consider the incorrect update 75, 97, 47, 61, 53. For the number 75, let’s look at the rules map and see how many of the rest of the numbers exist in the value slice for the key 75. All except 97, exist in the value slice. Lets do this for all numbers:

• 75 - count is 3 as 47, 61, 53 exist in its value slice.
• 97 - count is 4 as all numbers 75, 47, 61, 53 exist in its value slice.
• 47 - count is 2 as only 61 and 53 exist in its value slice.
• 61 - count is 1 as only 53 exists in its value slice.
• 53 - finally, count is 0 as none of the numbers in the update exists in its value slice.

The fixed update for the above is 97, 75, 47, 61, 53. Do you notice a pattern between the counts we observed above and the corrected update?

For an incorrect update, count of numbers found in the value slice for a given number is its index from the rear end, in the fixed update. This is because the count of numbers found in the value slice for a given number is the count of numbers that should come after the current number in the printing updates as per rules.

This makes our problem sufficiently easy to solve. All we need to do for an incorrect update is:

1. Iterate over each number.
2. For the current number, find count of numbers that exist in the value slice from all the numbers in the update.
3. New index of the current number is length of update - 1 - count.

Since we only need to find the middle number to compute final sum, as soon as we find the number that should be placed at the middle index, ie length of update / 2, we can exit. Putting it all together:

 func getMiddleNumberAfterFixingUpdate(update []int, ruleMap map[int][]int) int {
	fixedUpdate := make([]int, len(update))
	for i := 0; i < len(update); i++ {
		countFound := 0
		if _, ok := ruleMap[update[i]]; !ok {
			// means it should not come before any and should be last
			countFound = 0
		} else {
			// iterate over all the numbers in the update (except itself)
			// find count of all numbers that should come after it according to the rules
			for j := 0; j < len(update); j++ {
				if i == j {
					continue
				}
				found := false
				for _, element := range ruleMap[update[i]] {
					if element == update[j] {
						found = true
						break
					}
				}
				if found {
					countFound++
				}
			}
		}

		// the count of numbers that are found is the count of numbers that should come after it
		// so the current number's position = length of update - number of characters found
		// this is such that all the found characters have space to come after it.
		fixedUpdate[len(update)-countFound-1] = update[i]

		// if the middle number is found, exit early
		if fixedUpdate[len(update)/2] != 0 {
			return fixedUpdate[len(update)/2]
		}
	}
	return fixedUpdate[len(update)/2]
}

The sum of all middle numbers found after correcting the incorrect updates is the final answer! You can find my code here.

Alternative Approach

Part two is essentially a sorting problem. The rules given in the first section of the input are the sort rules. If we write a custom less function, we can make use of Golang’s slice.Sort method (ref) to solve the above in a couple of lines.

The custom less function will make use of the rules map we created earlier:

func customLess(ruleMap map[int][]int, update []int, i, j int) bool {
	if _, ok := ruleMap[update[i]]; ok {
		for _, char := range ruleMap[update[i]] {
			if char == update[j] {
				return true
			}
		}
	}
	return false
}

With the custom less function, we an solve both parts like below:

func alternativeAns(rulesMap map[int][]int, updates [][]int) (int, int) {
	sum, fixedSum := 0, 0
	for _, update := range updates {

		sortedUpdate := make([]int, len(update))
		copy(sortedUpdate, update)

		sort.Slice(sortedUpdate, func(i, j int) bool {
			return customLess(rulesMap, sortedUpdate, i, j)
		})

		if reflect.DeepEqual(update, sortedUpdate) {
			sum += update[len(update)/2]
		} else {
			fixedSum += sortedUpdate[len(update)/2]
		}
	}
	return sum, fixedSum
}

Elegant solution making use of standard library, what’s not to love!

This was the first day this year with a slightly difficult problem, especially in the second part. In hindsight it looks pretty obvious but arriving at this solution took me a while. But all’s well that ends well! And with that, Advent of Code day 5 is solved.

How was your experience solving Day 5? I would love to compare notes and checkout your solution. Reach out to me on Twitter, Bluesky or on e-mail at contact[at]shraddhaag[dot]dev.