Advent of Code Day 8 was quite easy, IF you read the problem statement correctly. This reminded me of the reading comprehensions in English exams back in school.

---

The below is a guest post by the amazing Shraddha Agrawal.

---

Part 1

The input is multiple rows of lines representing a 2D grid. A coordinate with a single lowercase letter, uppercase letter, or digit signifies an antenna with a specific frequency. All coordinates with the same character represent antennas with the same frequency.

Reading part 1 carefully, each pair of antennas with the same frequency will:

1. Create two “antinodes” which are equidistant and in line.
2. Only antinodes that are inbounds are considered valid.
3. Antinodes can occur at the location of other antennas (of same or different frequency).

Consider the following cases:

1. Case 1: The two antennas with 0 frequency placed diagonally from each other. The collectively produce 2 antinodes represented by #.
2. Case 2: We only get 1 valid antinode on the grid as the other one goes out of bound.
3. Case 3: Of the two antinodes, the left one overlaps with an antenna of another frequency. Both antinodes are valid.

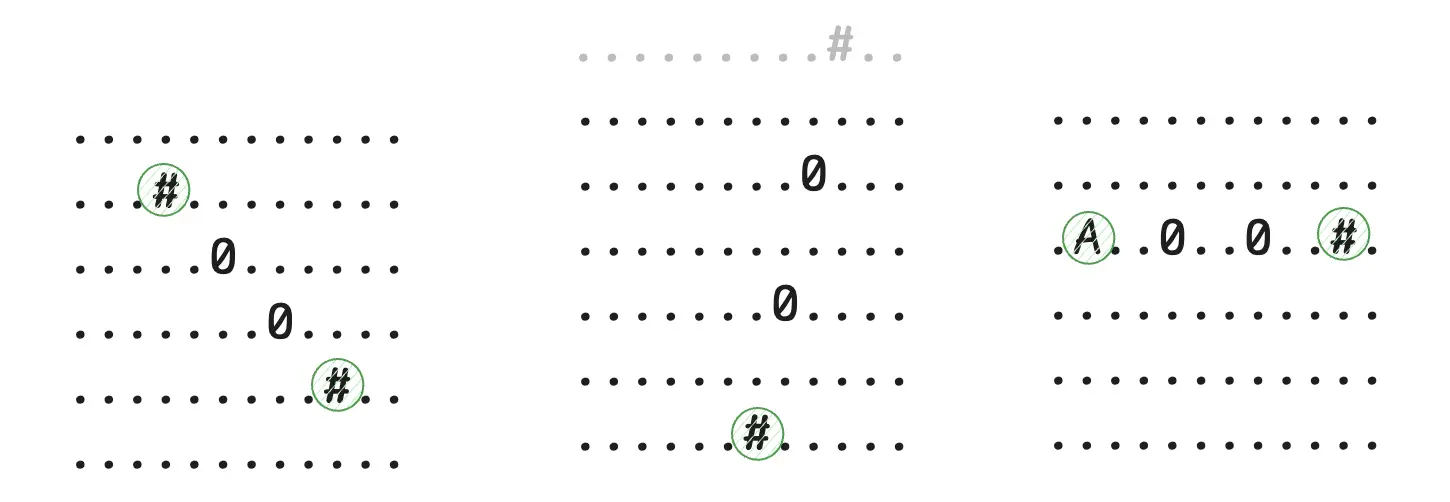
We need to return the total count of unique antinodes produced on the map by the given antennas.

Solution

The problem is fairly straightforward once understood. First, we need to figure out the location of each types of antennas. We will use a Golang map to store all locations for a given antenna frequency.

func findAllAntennas(input [][]string) map[string][]c {
	antennas := make(map[string][]c)
	for j, row := range input {
		for i, char := range row {
			if unicode.IsDigit(rune(char[0])) || unicode.IsLetter(rune(char[0])) {
				if _, ok := antennas[char]; !ok {
					antennas[char] = []c{{i, j}}
				} else {
					antennas[char] = append(antennas[char], c{i, j})
				}
			}
		}
	}
	return antennas
}

Now, for each pair of antennas, we need to figure out the antinodes’ coordinates. This can be done like below. The only thing to be careful of here is that the two coordinates of antinodes should be on the same line as the two antennas.

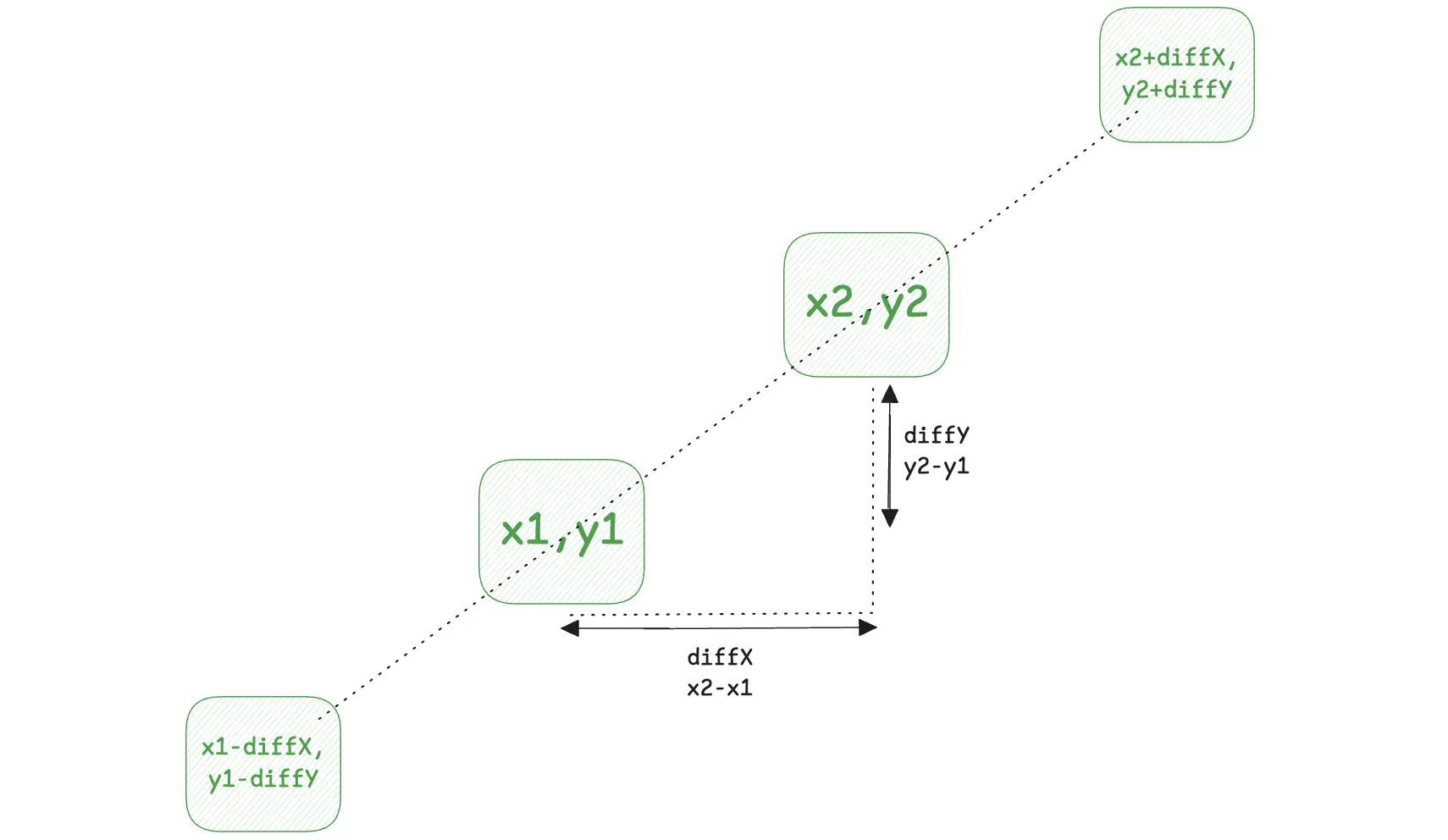
This can be implemented in code like this:

func calculateValidAntinode(a1, a2 c, maxX, maxY int, input [][]string) []c {
	validAntinode := []c{}
	diffX, diffY := a2.x-a1.x, a2.y-a1.y

	c1 := c{a1.x - diffX, a1.y - diffY}
	c2 := c{a2.x + diffX, a2.y + diffY}

	if isValidPosition(c1, maxX, maxY) {
		validAntinode = append(validAntinode, c1)
	}

	if isValidPosition(c2, maxX, maxY) {
		validAntinode = append(validAntinode, c2)
	}

	return validAntinode
}

Now, we just need to iterate over all the antennas found above and find distinct antinodes for all:

func countAntinode(input [][]string, antennas map[string][]c) (int, int) {
	maxX, maxY := len(input[0]), len(input)
	count1 := 0
	uniqueAntiNodes1 := make(map[c]struct{})
	for _, antenna := range antennas {
		if len(antenna) == 1 {
			continue
		}
		for i := 0; i < len(antenna)-1; i++ {
			for j := i + 1; j < len(antenna); j++ {
				validAntinodes := calculateValidAntinode(antenna[i], antenna[j], maxX, maxY, input)
				for _, antinode := range validAntinodes {
					if _, ok := uniqueAntiNodes1[antinode]; !ok {
						uniqueAntiNodes1[antinode] = struct{}{}
						count1++
					}
				}
			}
		}
	}

	return count1, count2
}

Part 2

The problem again was phrased confusingly. This time, for each pair of antennas with same frequencies, all equidistant, inline points are antinodes, including the antennas themselves.

Consider the below two antennas. With the updated rules will together generate 10 antinodes.

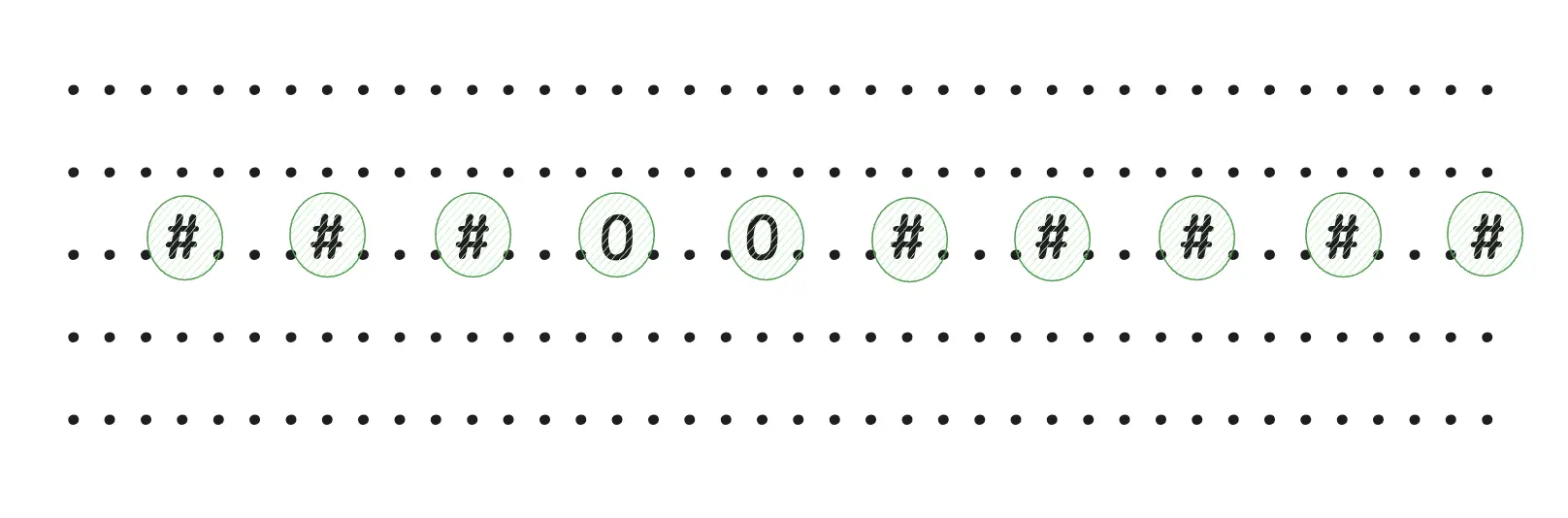
We again need return the total count of distinct antinodes now on the map.

Solution

All we need to do to solve this one is update our calculateAntiNode function such that now we find antinodes in a loop till both sides go out of bounds. Here, its important that we keep running the loop even if one side has gone out of bounds as there might be valid antinodes on the other side still. Also, another thing to keep in mind is that the original two antennas are also antinodes.

The updated function will look like:

 func calculateValidAntinode2(a1, a2 c, maxX, maxY int, input [][]string) []c {
	validAntinode := []c{a1, a2}
	diffX, diffY := a2.x-a1.x, a2.y-a1.y

	c1, c2 := a1, a2

	for isValidPosition(c1, maxX, maxY) || isValidPosition(c2, maxX, maxY) {
		if isValidPosition(c1, maxX, maxY) {
			validAntinode = append(validAntinode, c1)
		}

		if isValidPosition(c2, maxX, maxY) {
			validAntinode = append(validAntinode, c2)
		}

		c1 = c{c1.x - diffX, c1.y - diffY}
		c2 = c{c2.x + diffX, c2.y + diffY}
	}

	return validAntinode
}

Using this function, we can calculate the distinct count of antinodes for part two! Final code is available here.

Personally, I felt Day 8 was an apt simulation of a real life scenario of handling an incident. Taking the time to read and understand the problem always pays off while implementing the actual solution instead of hurrying to implement the correct solution to the wrong problem. This is true for both, solving such challenges and in actual production systems.

Did you understand Day 8 well? I would love to compare notes and checkout your solution. Reach out to me on Twitter, Bluesky or on e-mail at contact[at]shraddhaag[dot]dev.